Variación peso con la latitud

Datos

• Latitudes:
  • Quito: α_Q = 0º
  • México D.F: α_M = 19º= 0.33 rad
  • Buenos Aires: α_B.A. = 34º = 0.59 rad
• Masa persona m = 58 kg
• Intensidad del campo gravitatorio en la superficie g = g₀ = 9.8 N/kg
• Radio de la Tierra R_T = 6371 km = 6371·10³ m

Consideraciones previas

Observa que en el enunciado se nos dan latitudes norte (N) y sur (S). Esto en notación matemática hace referencia ángulos positivos y negativos de acuerdo a la siguiente imagen:

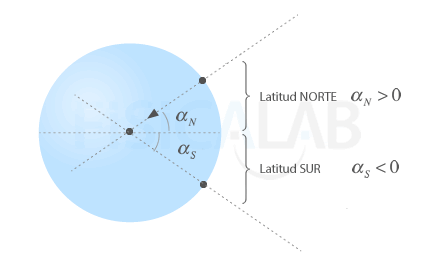
Sin embargo, para los cálculos que nos ocupan (el valor del peso, es decir, su módulo) y debido a la simetría respecto al ecuador, resulta indiferente que un cuerpo se sitúe a una determinada latitud norte o sur: El peso aparente será el mismo a 19º N que a 19ºS por lo que podemos obviar esta información y considerar todos los ángulos positivos.

Resolución

Debido a la fuerza centrífuga generada por la rotación de la Tierra, un cuerpo situado en su superficie experimentará una variación en el peso respecto al que tendía si se encontrara en reposo, tal y como se pone de manifiesto aquí. Al peso experimentado lo llamaremos peso aparente y podemos aplicar la siguiente expresión en el caso que nos ocupa

$${\overrightarrow{P}}_{aparente}=m·{\overrightarrow{g}}_{efectiva}\Rightarrow P_{aparente}=m·g_{efectiva}$$

Siendo en este caso la gravedad efectiva la aceleración que resulta de sumar vectorialmente la aceleración gravitatoria en la superficie (intensidad de campo en la superficie) con las aceleración centrífuga que surge del movimiento circular. 

El desarrollo para llegar a una expresión que nos permita calcular dicha gravedad efectiva en unas condiciones similares a las de este ejercicio ya se ha realizado en el apartado teórico al que corresponde. Aquí nos limitamos a recoger la expresión final:

$$\begin{gathered} {\overrightarrow{g}}_{efectiva}=\left({\omega }^2·R_T·\cos \left(\alpha \right)·\sin \left(\alpha \right)\right)·{\overrightarrow{u}}_h+\left({\omega }^2·R_T·{\cos }^2\left(\alpha \right)-g\right)·{\overrightarrow{u}}_v\Rightarrow \\ \Rightarrow g_{efectiva}=\sqrt{{\left({\omega }^2·R_T·\cos \left(\alpha \right)·\sin \left(\alpha \right)\right)}^2+{\left({\omega }^2·R_T·{\cos }^2\left(\alpha \right)-g\right)}^2} \end{gathered}$$

Ten bien presente que las expresión enterior sólo es válida si el cuerpo se sitúa en la superficie de la Tierra y en las condiciones expuestas. En caso de que estuviera, por ejemplo, a cierta altura (no desprecieable) tendríamos que realizar el desarrollo que se ajustara a las nuevas condiciones. Por otro lado, para determinar la velocidad angular de la Tierra, sabemos que da una vuelta completa (2·π rad) cada 24 horas (86400 s) por lo que:

$$\omega =\frac{2·\mathrm{\pi }}{86400}=7.2·{10}^{-5} rad/s$$

Finalmente, aplicando el valor correspondiente de α, podemos calcular el peso aparente en cada ciudad.

Quito

$$\begin{gathered} g_{efectiv{a}_Q}=\sqrt{{\left({\left(7.2·{10}^{-5}\right)}^2·6371·{10}^3·\cos \left(0\right)·\sin \left(0\right)\right)}^2+{\left({\left(7.2·{10}^{-5}\right)}^2·6371·{10}^3·{\cos }^2\left(0\right)-9.8\right)}^2}=9.76 m/s^2=9.76 N/kg\Rightarrow \\ \Rightarrow P_{aparent{e}_Q}=m·g_{efectiv{a}_Q}=58·9.76=566.08N \end{gathered}$$

México D.F.

$$\begin{gathered} g_{efectiv{a}_M}=\sqrt{{\left({\left(7.2·{10}^{-5}\right)}^2·6371·{10}^3·\cos \left(0.33\right)·\sin \left(0.33\right)\right)}^2+{\left({\left(7.2·{10}^{-5}\right)}^2·6371·{10}^3·{\cos }^2\left(0.33\right)-9.8\right)}^2}=9.77 m/s^2=9.77 N/kg\Rightarrow \\ \Rightarrow P_{aparent{e}_M}=m·g_{efectiv{a}_M}=58·9.77=566.66N \end{gathered}$$

Buenos Aires

$$\begin{gathered} g_{efectiv{a}_{B.A.}}=\sqrt{{\left({\left(7.2·{10}^{-5}\right)}^2·6371·{10}^3·\cos \left(0.59\right)·\sin \left(0.59\right)\right)}^2+{\left({\left(7.2·{10}^{-5}\right)}^2·6371·{10}^3·{\cos }^2\left(0.59\right)-9.8\right)}^2}=9.78 m/s^2=9.78 N/kg\Rightarrow \\ \Rightarrow P_{aparent{e}_{B.A.}}=m·g_{efectiv{a}_{B.A.}}=58·9.78=567.24N \end{gathered}$$