Decomposition of Forces

Sometimes, when we study the force acting on a body, it can be interesting to decompose it into several forces, each of them with the direction of the cartesian axis, in sucha a way the effect of all of them is equivalent to the force decomposed. As we study on the section vectors representation, on the plan OXY we get that:

$\vec{F} = \vec{F_{x}} + \vec{F_{y}} = F_{x} \cdot \vec{i} + F_{y} \cdot \vec{j}$

force decomposition in its cartesian components

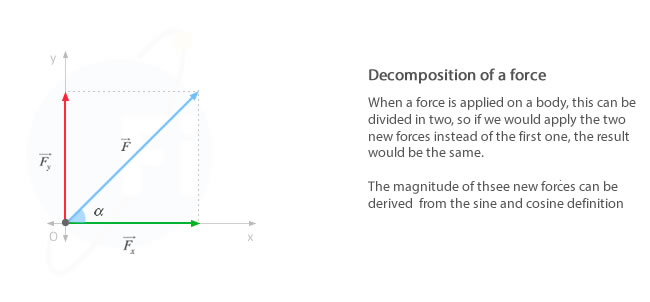
Taking into account the definition of vector magnitude, the magnitude of the force $\vec{F}$ is obtained throughout the following expression:

$F = \sqrt{{F_{x}}^{2} + {F_{y}}^{2}}$

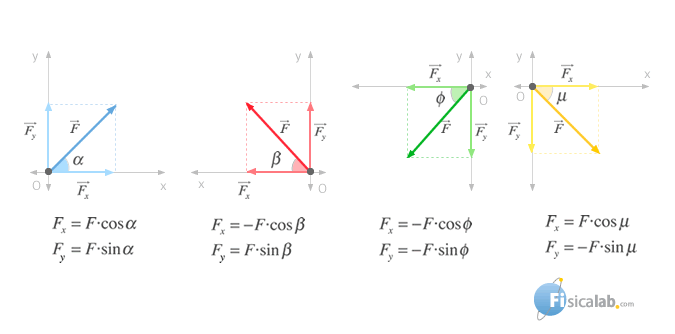
Throughout the definition of tangent of an acute angle we can relate the magnitudes F_x and F_y to the angle α that take place to with the half turn X positive on the following way:

$\tan (α) = \frac{F_{y}}{F_{x}}$

Additionally we can relate these magnitudes to the lower angle that make $\vec{F}$ with the X axis, pointing to the sector of the system of reference in which it is located:

Experiment & Learn

Data

Force vector decomposition

Drag the red point in order to change the force vector $\vec{F}$ from the figure. Watch how the value of its magnitude F decrese by making it smaller, and increase by making it bigger. The bigger magnitude, the higher force intensity.

Check how it can be decomposed into two forces $\vec{F_{x}}$ and $\vec{F_{y}}$ set over the coordinate axes, whose action together is equivalent to $\vec{F}$ . The value of the mgnitudes of these two forces are obtained throughout the use of the sine and cosine definition over the triangle rectangle which is formed, in such a way:

F_x = F · cos (α) = valor
F_y = F · sin(α) = valor

Example

A force is given by the following expression: $\vec{F} = 3 \cdot \vec{i} + 2 \cdot \vec{j}$ . Calculate angle of horizontal.

Solution

Now... ¡Test yourself!

Related sections

Site

Contact form

Follow us

Decomposition of Forces

Ayúdanos a mantenernos en órbita

¿Nuestros contenidos te están resultando de utilidad?

Now... ¡Test yourself!

Related sections