Momento lineal de varias partículas
Enunciado
Dos bolas de billar tienen la velocidades que se aprecian en la figura.
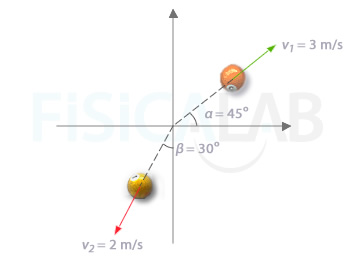
Sabiendo que m1 = 170 g y m2 = 156 g, calcula el momento lineal del sistema formado por ambas bolas.
Solución
Datos
- Masa de la primera bola: m1 = 170 g = 0.17 kg
- Valor (módulo) de la velocidad de la primera bola: v1 = 3 m/s
- Angulo con parte positiva del eje x del vector velocidad de la primera bola: α = 45º
- Masa de la segunda bola: m2 = 156 g = 0.156 kg
- Velocidad (módulo) de la segunda bola: v2 = 2 m/s
- Angulo con parte negativa del eje y del vector velocidad de la segunda bola: β = 30º
Consideraciones previas
Sabemos que el momento vectorial de un sistema de partículas (consideramos que las bolas de billar son partículas puntuales) se calcula como la suma de los momentos lineales de cada una de las partículas que lo componen. En este caso, para determinar estos momentos nos resultará conveniente tener la expresión vectorial de las velocidades de las bolas. Hay que tener cuidado, pues el ángulo α y el β están referidos a ejes distintos. Recuerda que, en general, consideraremos el semieje positivo x para los ángulos, quedando:
...y para el caso de la segunda velocidad tendremos en cuenta que el ángulo a considerar será también el que forma el vector con el semeje positivo x, es decir 270º - 30º = 240º(como se deduce de la propia figura):
Resolución
La cantidad de movimiento total del sistema es la suma de las cantidades de movimiento de ambas bolas, es decir:
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
