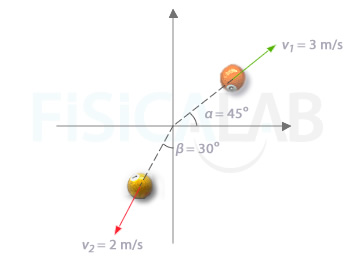
Statement
Two pool balls have the following velocity:
Knowing that m1 = 170 g y m2 = 156 g, calculate the system´s linear momentum formed by both balls.
Solution
Data
- Mass of the first ball: m1 = 170 g = 0.17 kg
- Value (magnitude) of the first´s ball velocity: v1 = 3 m/s
- Angle with positive side of the axis x of the velocity vector of the first ball: α = 45º
- Mass of the second ball: m2 = 156 g = 0.156 kg
- Velocity (magnitude) of the second ball: v2 = 2 m/s
- Angle with negative side of the axis and the velocity vector of the second ball: β = 30º
Previous considerations
We know the vector momentum of a system of particles (we consider the pool balls as particles) is calculated as the sum of linear momentums of each of the particles is made of. On that case, to determine those momentums it would be good to have the vector expression of the ball´s velocities. Watch out, because the angle α and the β are refered to different axis. Remember that, in general, we considerthe positive semi-axis x for the angles, so:
... and for the case of the second velocity we will have into account that the angle to consider will be also the one making the vecto with positive semi-axis x = 270º - 30º = 240º(as we can find out on the figure):
Resolution
The quantity of total motion of the system is the sum of the quantities of motion of both balls, so: