Campo eléctrico creado por un anillo de carga uniforme

Para resolver este ejercicio vamos a dividir el anillo en pequeñas porciones infinitesimales de carga, cada una de las cuales influirá en la creación del campo eléctrico en cualquier punto P situado a lo largo del eje del anillo. La simetría que posee el anillo, hace que solo influyan las componentes x del campo eléctrico (dE_x, dE_x', ...) ya que las componentes y se anulan (dE_y, dE_y',...). Por tanto, nos centraremos en calcular la suma de todas las primeras.

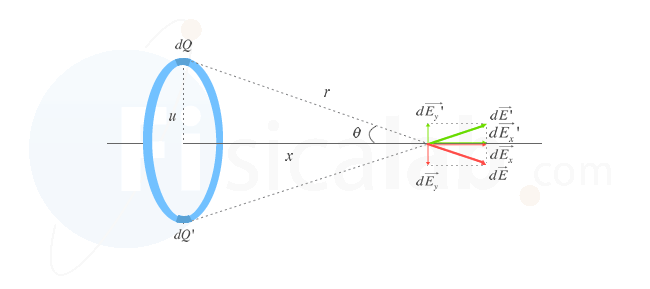
Para ello, calcularemos el valor de la componente x del campo eléctrico creado por dQ, aplicando la definición de coseno:

$$d{E}_x=dE·\cos \theta$$

Adicionalmente, si consideramos el campo creado por una carga puntual y que según la figura cos Θ = x/r

$$d{E}_x=K·\frac{dQ}{r^2}·\frac{x}{r}$$

Nuevamente, aplicando el teorema de Pitágoras al triángulo que resulta de la figura:

$$d=\sqrt{x^2+u^2}$$

Por tanto:

$$\begin{gathered} d{E}_x=K·\frac{dQ}{\sqrt{{\left(x^2+u^2\right)}^2}}·\frac{x}{\left(x^2+u^2\right)}\Rightarrow \\ d{E}_x=K·\frac{dQ·x}{{\left(x^2+u^2\right)}^{3/2}} \end{gathered}$$

Partiendo de esta ecuación deseamos calcular el campo creado por cada una de las cargas situadas a lo largo del anillo, por esta razón vamos a darle una vuelta y a expresarla en función de la longitud del anillo:

$$dQ=\lambda ·dl$$

Ahora podemos integrar a lo largo de dicha longitud:

$$E={\int }_0^{2\pi u}K\frac{\lambda ·dl·x}{(x^2+u^2{)}^{3/2}}$$

Resolviendo la integral:

$$\begin{gathered} E={\int }_0^{2\pi u}K\frac{\lambda ·dl·x}{(x^2+u^2{)}^{3/2}}\Rightarrow \\ E=K\frac{\lambda ·x}{(x^2+u^2{)}^{3/2}}{\int }_0^{2\pi u}dl \Rightarrow \\ E=K\frac{\lambda ·x}{(x^2+u^2{)}^{3/2}}·2·\pi ·u \end{gathered}$$

Dado que λ=Q/2·π·u :

$$E=K\frac{Q·x}{(x^2+u^2{)}^{3/2}}$$

Una vez que conocemos la expresión del campo eléctrico a cualquier distancia x del eje del anillo, vamos a responder a las preguntas que nos solicitan en el ejercicio:

• En el centro del anillo x = 0, por tanto si sustituimos en la expresión del campo eléctrico obtendremos que E = 0.
• En un punto situado muy lejos x>>>u obtendremos que E = K· Q / x², es decir, a una distancia extremadamente grande el anillo se comporta como si se tratase de una carga puntual.