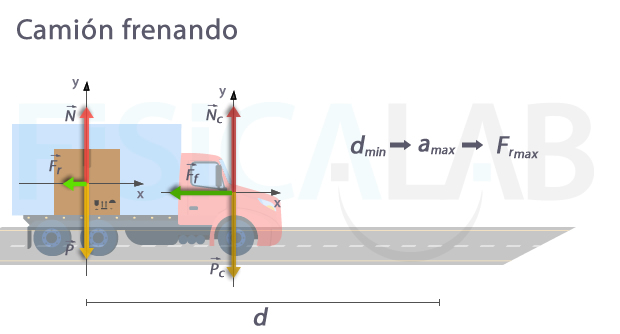
Desplazamiento de caja en camión

Consideraciones previas

Para resolver este problema aplicaremos el procedimiento para resolver problemas de fuerzas ya estudiado. Nos centraremos en estudiar las cajas (haremos los cálculos para una sola caja, ya que si una se desplaza, las demás también lo harán). Situaremos nuestro "observador" en un punto fijo fuera del camión, estudiando así la situación desde un sistema de referencia en reposo, esto es inercial. Podemos entonces distinguir dos situaciones:

• Mientras el camión se desplaza con velocidad constante, también lo hacen las cajas. Sabemos, por la primera ley de Newton que la resultante de todas las fuerzas que actúen sobre la caja deben ser cero (pues la velocidad permanece constante).

  

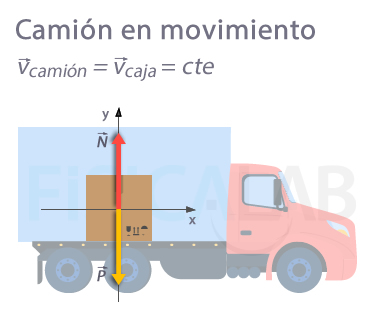
  Diagrama del cuerpo libre con velocidad constante

  • En el eje y se cumple, pues el peso y la normal coinciden
  • En el eje x podemos suponer que no actúan fuerzas. Para ser precisos, actuarían algunas fuerzas disipativas en el sentido negativo del eje x, que serían compensadas por la fuerza de rozamiento estática actuando, con igual valor, en el sentido positivo del eje

• Cuando el camión comienza a detenerse. En este caso, el camión aplica sus frenos (fuerza F_f), y aparece una aceleración contraria al sentido del movimiento (podemos decir, negativa), que hace que el camión se detenga al recorrer una determinada distancia. Se trata de un m.r.u.a. En el caso de la caja, es justamente la fuerza de rozamiento entre la caja y el camión la responsable de que la caja también se detenga, al aparecer una aceleración también de sentido contrario al movimiento de la caja. Si esta aceleración tiene distinto valor que el de la aceleración del camión, se producirá un desplazamiento.

  

  Diagrama del cuerpo libre al aplicar frenos

  Cuano se aplican frenos, aparece una fuerza F_f sobre el camión que se transmite a la caja debido a las rugosidades de las superficies y las características de los materiales (superficie camión - caja). Se genera así una fuerza de rozamiento F_r sobre la caja. Lo importante es que te percates de que la distancia d mínima que puede recorrer la caja sin desplazarse respecto al camión será la que ocurra cuando la aceleración a de la misma sea la máxima posible. A su vez, esta aceleración será la máxima cuando la fuerza de rozamiento F_r alcance su valor máximo (pues F=m·a). El valor máximo que alcanza la fuerza de rozamiento es F=μ·N.

  Por otro lado, observa que lo que deben ser iguales son las aceleraciones que aparecen en el camión y en la caja. No así las fuerzas que aparecen, ya que la caja y en el camión no tienen por qué tener la misma masa.

Por último, ten presente que tendremos en cuenta el criterio de signos coincidente con los ejes (que a su vez coincide en este caso con el sentido del movimiento).

Datos

• v₀=54 Km/h=15 m/s
• v_f=0
• μ=0'3
• g=9'8 m/s²

Resolución

Aplicando la segunda ley de Newton y la expresión para la fuerza de rozamiento máxima a la caja, y que la fuerza total que actúa en el eje x es justamente la fuerza de rozamiento podemos obtener el valor de la aceleración máxima:

$$\begin{gathered} F_T=m·a ; F_r=-\mu ·N=-\mu ·m·g ;\hspace{0.17em}{F}_T=F_r \\ \cancel{m}·a=-\mu ·\cancel{m}·g\Rightarrow a=-\mu ·g=-0.3·9.8=-2.94 m/s \end{gathered}$$

Una vez conocida la aceleración:

$$a=\frac{v_f-v_0}{t}\Rightarrow t=\frac{0-15}{-2.94}=5.1 s$$

Ya conocemos el tiempo que tarda en detenerse el camión con la caja, ahora se reduce a un problema de cinemática. Sabiendo que se produce un movimiento rectilinieo uniformemente acelerado, tenemos todo para poder despejar la distancia.

$$x=v_0·t+\frac{1}{2}·a·t^2\Rightarrow x=15·5.1+\frac{1}{2}·\left(-2.94\right)·5.1^2\Rightarrow \boxed{x=51.3 m}$$