Suma de vectores básica
Enunciado
Dados los siguientes vectores:
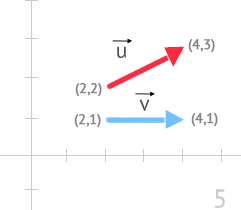
Calcula en el siguiente orden:
a) La representación gráfica de la suma de ambos vectores.
b) La representación analítica de la suma de ambos vectores.
c) La representación analítica del opuesto del vector u
d) ¿El módulo de la suma de dos vectores es igual a la suma de los módulos de cada vector individualmente?
Solución
Cuestión a)
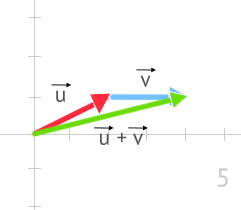
Lo que se nos pide en este ejercicio, es representar gráficamente el vector resultante de sumar u y v que denotaremos como u+v.
Tal y como hemos visto, la suma de vectores desde un punto "gráfico" se puede resolver mediante 2 métodos:
- Método de la cabeza con cola.
- Regla del Paralelogramo.
Para representar u+v, usaremos la primera de ellas.
- Desplazamos u de forma que su punto de origen coincida con el origen de coordenadas y mantenemos, su dirección, módulo y sentido.
- Desplazamos v de forma que su punto de origen coincida con el extremo del vector u, manteniendo igualmente su dirección, módulo y sentido.
- Trazamos un vector u+v cuyo punto de aplicación es el punto de origen de u y su extremo es el punto de extremo de v.
Cuestión b)
En este apartado, lo que se nos pide es la ecuación del vector resultado de sumar u y v. El cálculo de dicha ecuación resulta más fácil si disponemos de las ecuaciones de u y v, sin embargo no nos las proporcionan en el ejercicio. De lo que si disponemos es de los puntos origen y extremos, lo que es muchísima información ya que a partir de ellos podemos obtener las ecuaciones de u y v.
vector u
Llamaremos UO al punto origen y OE al punto extremo del vector u. Observando la gráfica podemos determinar que UO = (2,2) y UE = (4,3). Aplicando la definición de vector:
vector v
Para este vector, repetiremos los mismos pasos que para el vector u, aunque en esta ocasión llamaremos VO a su punto de origen y VE al extremo. Si nuevamente nos centramos en la gráfica, podemos deducir que VO= (2,1) y VE= (4,1). Aplicando la definición de vector:
En resumen, hemos obtenido la siguiente representación analítica de u y v
De aquí podemos obtener las componentes cartesianas de ambos vectores y que nos servirán para calcular la suma:
Sustituyendo en la definición de suma de vectores que hemos visto en el desarrollo del tema, el vector u + v será:
Cuestion c)
Para calcular el opuesto de un vector, basta con cambiar el signo de las componentes de dicho vector. Por lo tanto si
entonces su opuesto se representa de la siguiente forma:
Cuestion d)
En este punto lo que nos está preguntando es ¿
Para poder comprobarlo, vamos a calcular los módulos que nos solicitan:
Si hacemos las operaciones pertinentes nos damos cuenta de que aunque parece que son valores muy parecidos, el modulo de la suma de los dos vectores no es igual a la suma de sus módulos. De hecho, de forma general, si los vectores no tienen la misma dirección:
No hemos encontrado ninguna fórmula destacable en este ejercicio.
