Límite de una Función en un Punto
De manera intuitiva, el límite de una función real en un punto 'a' es el valor L al que se aproxima la función (es decir, su coordenada y) a medida que la coordenada x se aproxima a a. En la siguiente imagen queda recogido el concepto y la notación que se suele utilizar:
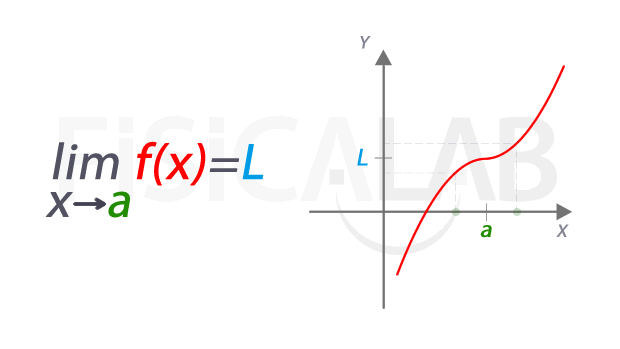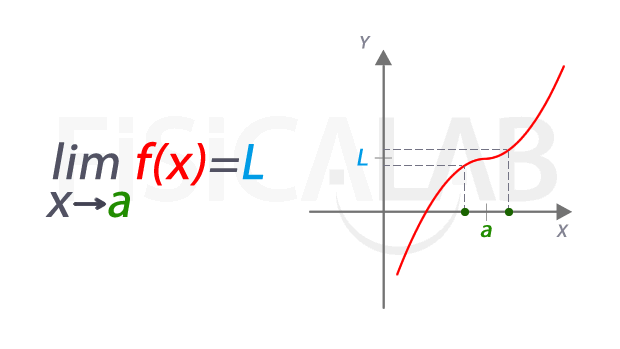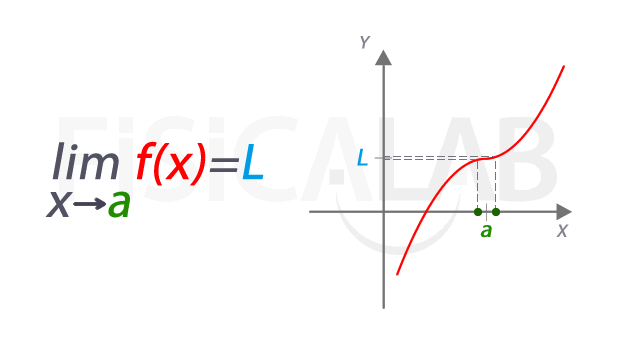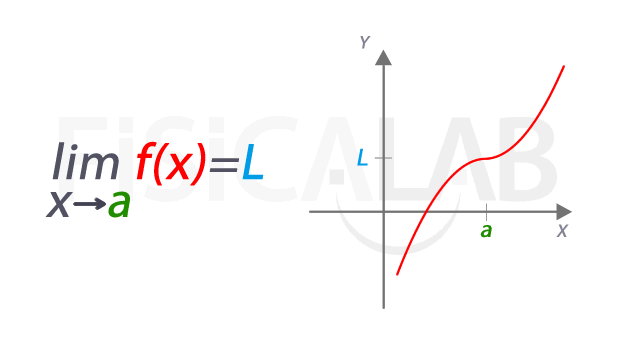
Concepto de límite de una función en un punto
A la izquierda la notación empleada para referirnos al límite. Se lee "límite de f(x) cuando x tiende a a" . El valor del límite es L, representado en azul. La función f(x) está en rojo, y el punto en el que estamos estudiando el límite tiene una coordenada x cuyo valor es a, en verde. A la derecha esta misma idea representada de manera dinámica. A medida que nos acercamos a x=a, las correspondientes imágenes se aproximan al valor del límite L. Aunque en este caso, el valor del límite coincide con el de la función en el punto, pues f(a)=L, en realidad se trata de dos conceptos distintos, como veremos más abajo.
En este apartado vamos a profundizar en esta idea. Para ello empezaremos aproximándonos al concepto de una manera intuitiva, presentaremos distintos ejemplos y terminaremos con una definición formal. Lo haremos a través de los siguientes puntos:
- Concepto de aproximaciones sucesivas
- Límites por la izquierda y por la derecha
- Límite de una función en un punto
- Definición formal
- Propiedades
- Conclusiones
Si lo que deseas es aprender a calcular el límite de una función en un punto, y ya estás familiarizado con este concepto, te recomendamos que vayas directamente al apartado enlazado.
¿Preparado para estudiar "al límite"?
Aproximaciones sucesivas
Imagina que te pedimos que recorras la mitad de la distancia que te separa de la puerta de tu habitación. Una vez allí, te pedimos que lo hagas de nuevo... y una vez allí, una vez más... ¿Llegarías finalmente a recorrer la distancia que te separaba de la puerta al principio si seguimos dándote, una y otra vez, la misma orden?
Lo cierto es que en cada iteración te aproximarías al valor de la distancia total, y, si repitieras el proceso infinitas veces, efectivamente, lo alcanzarías. Apliquemos a una función esta idea de aproximarnos sucesivamente a un punto:
¿Qué valor alcanza la función (es decir, su coordenada y) cuando la x se aproxima a 3?
Tu primera tentación puede ser intentar calcular f(3)... pero vemos que queda 0/0, y ya sabemos que no tiene sentido en matemáticas dividir entre 0 (y mucho menos si el número que divido es el propio cero). Pero observa qué ocurre cuando hacemos varias aproximaciones sucesivas:
| x | y=f(x) |
| 2 | 0.5 |
| 2.5 | 0.75 |
| 2.9 | 0.95 |
| 2.99 | 0.995 |
| 2.999 | 0.9995 |
A medida que me aproximo a x=3, sin llegar a alcanzarlo, el valor de la función se aproxima a 1. Observa que todos los valores de x que hemos tomado eran ligeramente menores que tres. Podemos repetir el proceso, tomando esta vez valores ligeramente mayores que tres:
| x | y=f(x) |
| 4 | 1.5 |
| 3.5 | 1.25 |
| 3.1 | 1.05 |
| 3.01 | 1.005 |
| 3.001 | 1.0005 |
Como vemos, la sucesión de valores también nos conduce a 1. Por tanto, podemos decir que 1 es el límite de
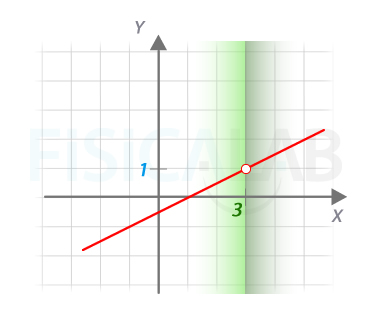
Ejemplo de límite de una función
En rojo, gráfica de la función del ejemplo,
Aunque decimos "límite de una función en un punto", cuando calculamos el límite lo que hacemos es estudiar si las imágenes de la función se acercan a un valor concreto cuando la variable independiente x "tiende a" a (o "se acerca a" a). Dicho de otra manera, el límite es un concepto dinámico.
Límites por la izquierda, por la derecha y límite de la función
Para determinar el valor del límite del ejemplo hemos seguido en realidad un doble camino:
- Nos hemos acercado a x=3 por la izquierda, es decir, tomando valores ligeramente menores que 3, y...
- nos hemos acercado también por la derecha, es decir, tomando valores ligeramente superiores a 3
Como ambos procesos nos llevaban al mismo valor de la función, concluíamos que
El valor del límite de una función f(x) cuando x tiende a a por la izquierda es el valor al que se acerca y=f(x) cuando x se acerca a a tomando valores menores que a. Se denota:
Donde:
- f(x) : es la función cuyo límite por la izquierda estoy calculando
- L : Es el valor del límite lateral. Puede ser un número real cualquiera, pero también infinito ∞ o menos infinito -∞
Observa algunos ejemplos:
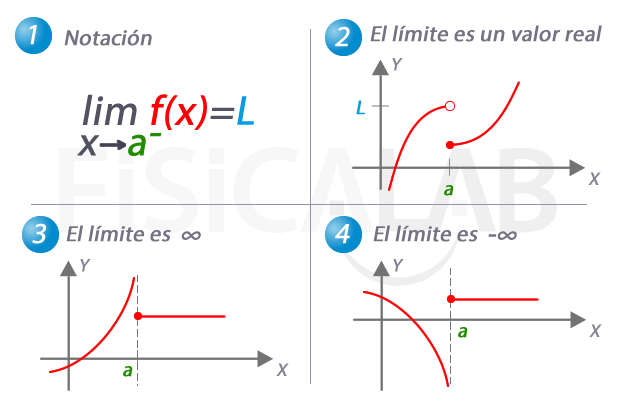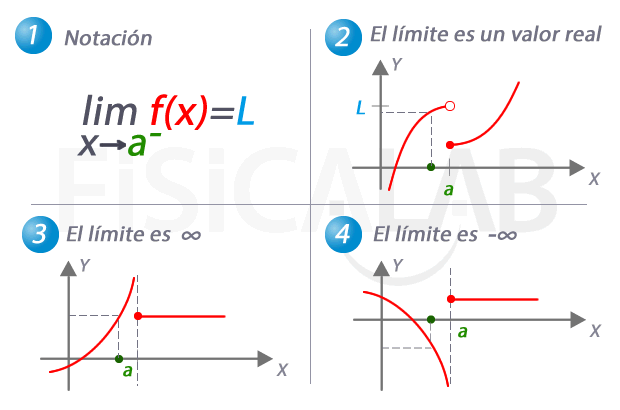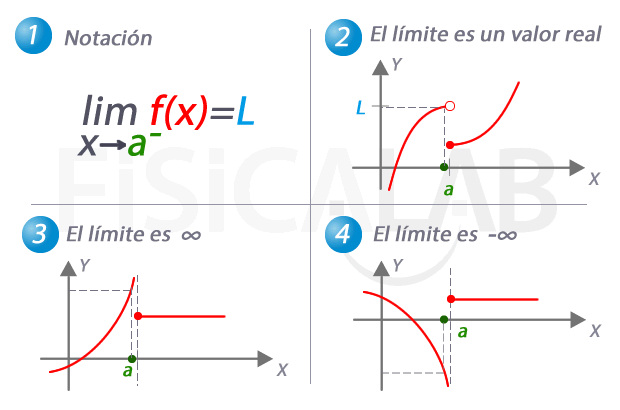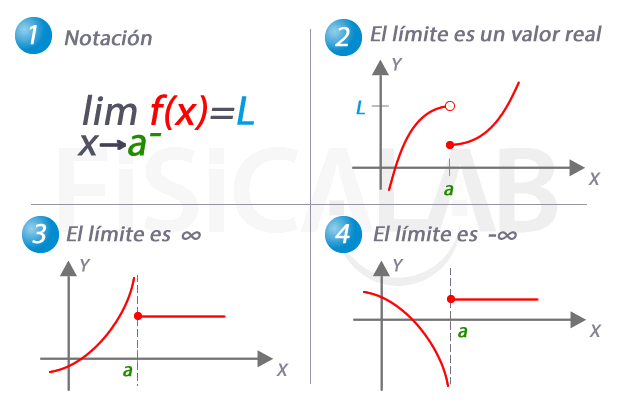
Límite lateral por la izquierda de una función
En 1, la notación utilizada para referirnos al límite de una función cuando x se aproxima a a por la izquierda. En 2, 3 y 4 tenemos tres ejemplos distintos. En 2 el límite es una valor real concreto, L. Observa como, de nuevo, el valor del límite no coincide con el de la función en el punto. En 3, a medida que nos aproximamos a a por la izquierda, los correspondientes valores de y son cada vez mayores. Es el caso en el que el valor del límite lateral es infinito. En 4, el caso complementario, con un límite lateral de menos infinito.
El valor del límite de una función f(x) cuando x tiende a a por la derecha es el valor al que se acerca y=f(x) cuando x se acerca a a tomando valores mayores que a. Se denota:
Donde:
- f(x) : es la función cuyo límite por la derecha estoy calculando
- L : Es el valor del límite lateral. Puede ser un número real cualquiera, pero también infinito ∞ o menos infinito -∞
Observa algunos ejemplos:
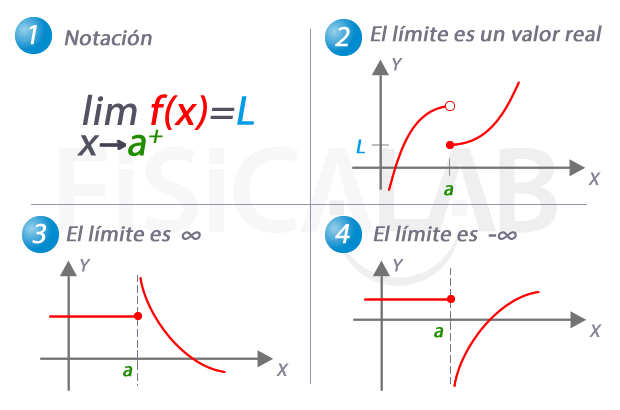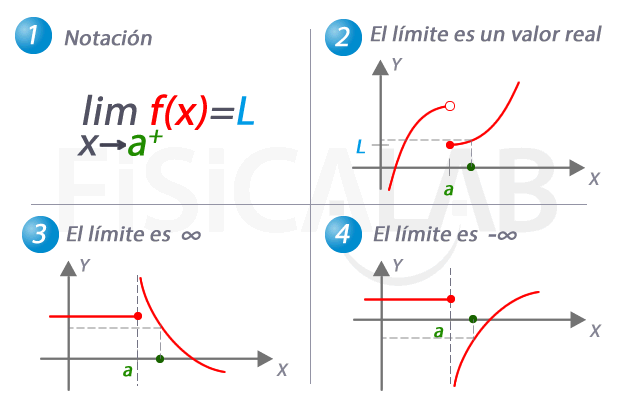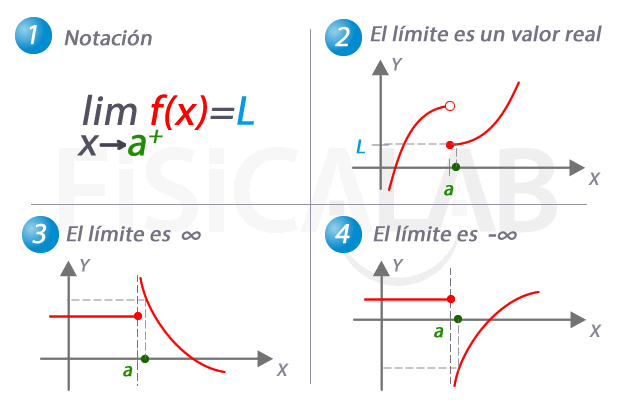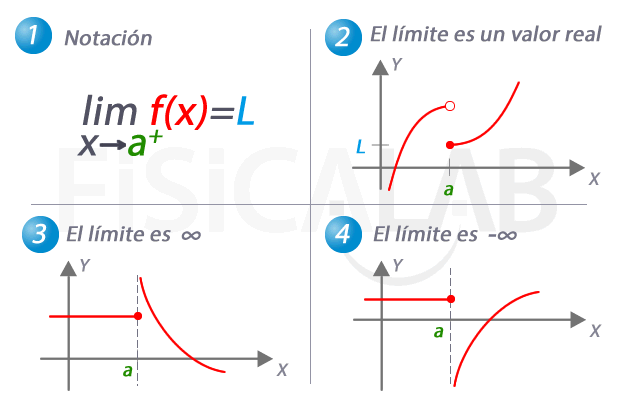
Límite lateral por la derecha de una función
En 1, la notación utilizada para referirnos al límite de una función cuando x se aproxima a a por la derecha. En 2, 3 y 4 tenemos tres ejemplos distintos. En 2 el límite es una valor real concreto, L. Observa como, de nuevo, el valor del límite coincide en este caso con el de la función en el punto. En 3, a medida que nos aproximamos a a por la derecha, los correspondientes valores de y son cada vez mayores. Es el caso en el que el valor del límite lateral es infinito. En 4, el caso complementario, con un límite lateral de menos infinito.
Límite de una función en un punto
La condición necesaria y suficiente para que exista el límite de una función en un punto es que ambos límites laterales existan y sean iguales. Entonces decimos que el límite existe y tiene ese mismo valor:
Donde:
- f(x) : Es la función cuyo límite estamos calculando
- L : Es el valor del límite, que debe coincidir con los límites laterales. Puede ser un número real cualquiera, pero también infinito ∞ o menos infinito -∞
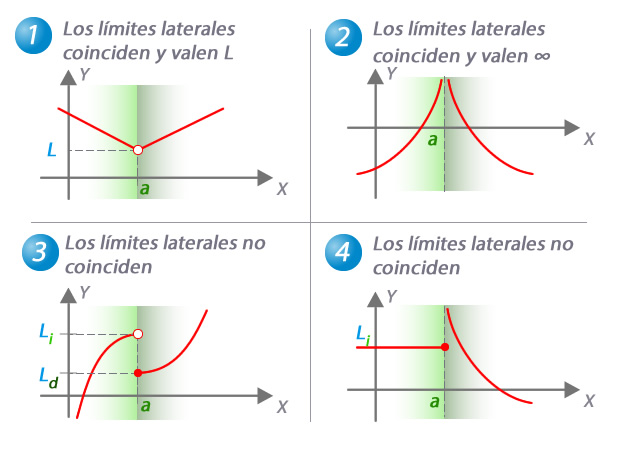
Coincidencia de límites laterales
En 1 y 2 dos ejemplos de funciones cuyos límites laterales en x=a coinciden, con lo que el límite de la función existe y tiene igual valor que estos. En 2 y 3 los límites laterales no coinciden, con lo que no existe el límite de la función en x=a. Así:
- 1:
- 2:
- 3:
- 4:
Aunque estrictamente hablando no existe el límite cuando los límites laterales son distintos, por convención si un límite lateral es +∞ y el otro -∞ decimos que el límite de la función en el punto es ∞.
Definición formal
Con las ideas más o menos intuitivas vistas hasta ahora, ya estamos en disposición de estudiar el cálculo de algunos límites. Sin embargo, puede que hayas venido a parar aquí buscando una definición formal de lo que es un límite en matemáticas, y no vamos a decepcionarte, aunque insistimos, no es necesario que la aprendas para seguir avanzando en este nivel educativo. Iremos desarrollando ideas de más intuitivas y menos formales a menos intuitivas y más formales.
Hemos dicho que el límite de una función f(x) cuando x tiende a a es L si a medida que tomo valores más próximos a a, los correspondientes valores de f(x) son más próximos a L. Esto es:
Pero... ¿qué significa exactamente "tender a 0"? Podemos formalizar esta idea a partir de la noción de entorno. Recuerda que un entorno de centro a y radio r es un intervalo abierto de valores próximos a dicho número real y que lo contiene, es decir,
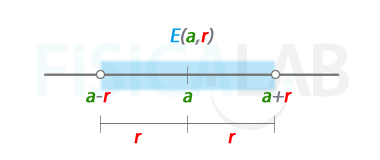
Entorno de centro a y radio r
Representación gráfica de un entorno con centro a y radio r. Es un intervalo abierto en el que la distancia entre el centro a y los extremos es r.
Decimos que
La siguiente imagen te lo aclarará:
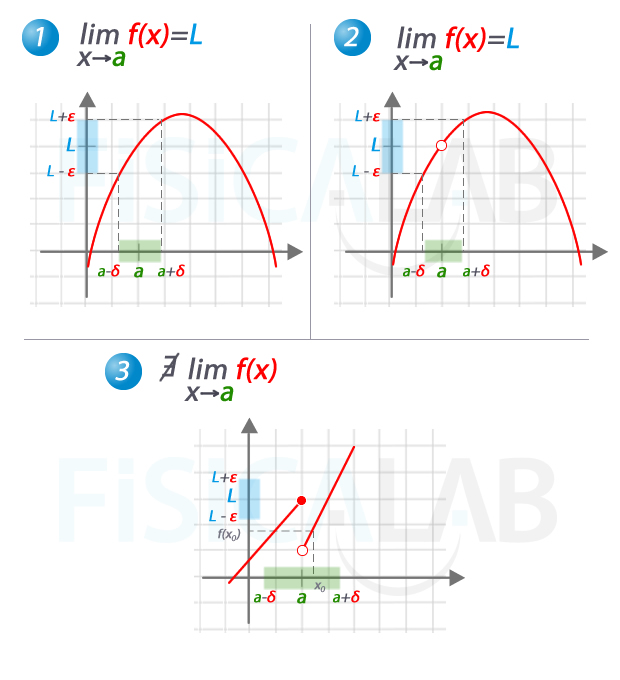
Elementos de la definición de límite de una función en un punto
En la imagen se muestran los elementos propios de la definición formal de límite en tres casos distintos. Fíjate, en primer lugar en 1. El entorno de centro L y radio ε ha sido representado en azul claro. A dicho entorno podemos hacer corresponder, en el eje x, un entorno de centro a y radio δ, en verde claro, cuyos elementos tienen todas sus imágenes en el interior del entorno de centro L del eje y. Observa que, si escogiéramos un ε menor, el entorno correspondiente del eje x seguiría cumpliendo esta condición. De ahí que se diga en la definición "para cualquier entorno de L". En definitiva, es por eso que decimos que
Por otro lado, en 2, se pone de relieve que la función no tiene porque estar definida en a, de ahí que se diga en la definición "sin importar lo que ocurra en a".
Finalmente, en 3, tenemos una función cuyo límite no existe en a. Observa que, dado un entorno de L, hemos encontrado en el correspondiente entorno de a un elemento, x0 cuya imagen f(x0) no está en el primer entorno, luego la condición exigida no se cumple "para cualquier" entorno de L.
Finalmente, como hemos dicho antes un entorno puede ser expresado como una desigualdad con valor absoluto, según E(r,a)=|x-a|<r, con lo que podemos llegar a la misma idea prescindiendo de la noción de entorno:
La definición formal de límite, también llamada definición de Cauchy afirma que
Donde:
Observa en las definiciones anteriores no nos permiten calcular el valor del límite, pero sí, una vez conocido este, comprobar si lo es o no.
Si una función tiene límite en un punto, este es único.
Propiedades
Supongamos que
-
El límite de la función en el punto es único
-
La función queda acotada en un entorno reducido de a
-
Si L≠0, entonces existe un entorno reducido de a en el que el signo de f(x) es el mismo que el del límite L
-
Si dos funciones f(x) y g(x) tienen límite cuando x tiende a a y además toman los mismos valores en un entono reunido de a, entonces tienen el mismo límite, es decir,
Conclusiones
En este apartado hemos presentado y hemos profundizado en el estudio del límite de una función en un punto. Lo hemos hecho partiendo de una idea intuitiva y hemos llegado a una definición rigurosa y formal del mismo. Los límites son herramientas fundamentales para el estudio de la continuidad de las funciones. En apartados posteriores vamos a estudiar como realizar el cálculo de los mismos, ya que la definición que hemos visto no nos dice cómo hacerlo, estudiaremos a fondo sus propiedades y practicaremos todo ello a través de nuestras listas de ejercicios resueltos. ¿Seguimos o tomamos un descanso?
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
