Ramas Parabólicas de una Función
Una función tiene una rama parabólica si al crecer indefinidamente la x (por la izquierda o por la derecha), crece indefinidamente la función (por arriba o por abajo), pero sin acercarse a ninguna recta en particular. Las ramas parabólicas no son asíntotas de ningún tipo. Más formalmente:
Decimos que una función presenta una rama parabólica cuando no presenta una asíntota oblicua, pero se cumple:
Donde
- x→∞: Puede ser también x→-∞
- f(x): Es la función que presenta la rama parabólica
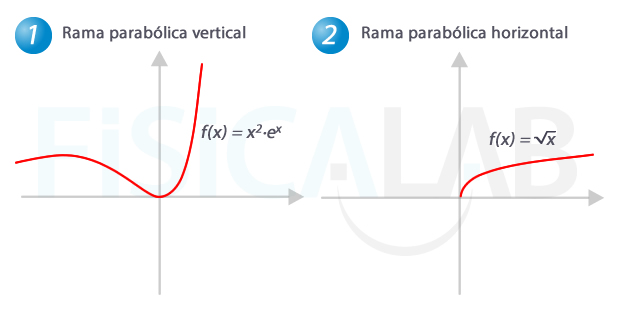
Ramas parabólicas
Gráficamente una función que posee una rama parabólica se comporta como si formase parte de una parábola de eje vertical, oblicuo u horizontal. En 1, función con rama parabólica en la dirección del eje y (vertical). En 2, función con rama parabólica en la dirección del eje x (horizontal).
Tipos
Más concretamente podemos distinguir tres casos:
-
Rama parabólica con eje horizontal
-
Rama parabólica con eje vertical
-
Rama parabólica con eje oblicuo y=x
Donde en todos los casos x→∞ puede ser también x→-∞
En funciones racionales
Hay ramas parabólicas en aquellas funciones racionales, f(x)=P(x)/Q(x), en las que el grado del numerador está dos unidades o más por encima del grado del denominador.
Ejemplo
En la función
...entonces la función presenta una rama parabólica hacia arriba en +∞ y otra en -∞. Concretamente se trata de ramas verticales, ya que:
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
