Asíntotas de una Función
Una asíntota es una recta a la cual se aproxima indefinidamente una función, sin llegar nunca a tocarla.
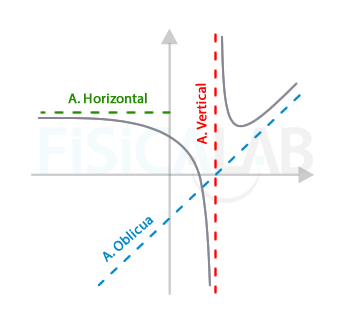
Tipos de asíntotas
La palabra asíntota proviene del griego asumptotos que significa sin encontrarse. En la figura tenemos los 3 tipos de asíntotas que puede presentar una función: en verde, una asíntota horizontal; en rojo, una asíntota vertical; en azul, una asíntota oblicua. Como puedes ver, las ramas de la función nunca tocan a las asíntotas, pero se aproximan de manera constante a ellas.
Como ves, gráficamente las asíntotas se asocian a ramas de la función infinitas (que no tienen fin). En este apartado aprenderemos a calcular:
Además ilustraremos todo ello con varios ejemplos. ¿Empezamos?
Ya sabes que, en matemáticas, para indicar que una función se aproxima a un valor se utiliza el concepto de límite, de ahí su importancia para el cálculo de las asíntotas.
Asíntotas verticales
Decimos que la recta x=k es una asíntota vertical de la función f(x) cuando se cumple:
Donde:
- k: es el valor real del eje x al que se aproxima la función de forma indefinida, ya sea por la izquierda o por la derecha del mismo. Por ejemplo, -2,0 ó 1. Se dice que la función diverge en x=k
- f(x): Es la función que presenta la asíntota
Por tanto, para saber si una función presenta asíntotas verticales en un punto, habría que estudiar el límite en él. Basta con que solo uno de los límites laterales exista, para que consideremos x=k una asíntota vertical.
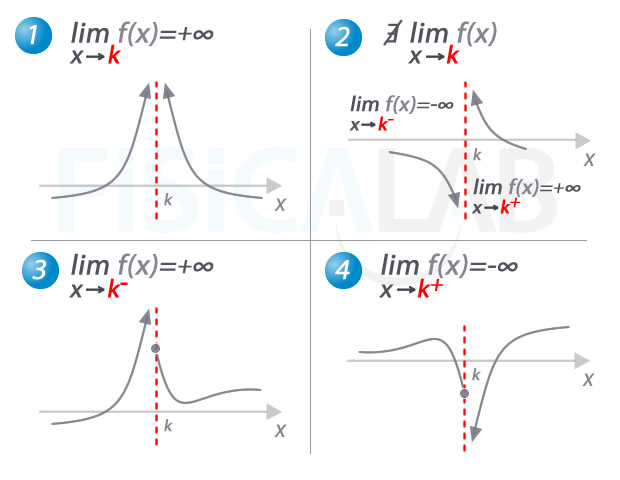
Asíntotas verticales
Gráficamente, las asíntotas verticales se distinguen porque, a medida que nos acercamos a un valor concreto de x, la función "se va" a infinito (o a menos infinito). En 1 los límites laterales, y por tanto el límite, de la función es infinito. En el segundo caso, los límites laterales son distintos, por lo que no existe, estrictamente hablando, el límite, aunque sí la asíntota. En 3 y 4 podemos ver que basta que sólo uno de los límites laterales sea infinito para que exista la asíntota.
Cálculo en funciones racionales
Ya sabes que una función racional es aquella que se puede expresar como el cociente de dos polinomios: f(x)=P(x)/Q(x). En estos casos:
- Simplificamos f(x) factorizando P(x) y Q(x) y eliminando las raíces comunes
- Las raíces del denominador son las asíntotas verticales de f(x), con lo que las buscamos haciendo Q(x)=0
Ejemplo
Para calcular las asíntotas verticales de
Como no hay raíces comunes, no es necesario simplificar. Resolvemos Q(x)=0:
Con lo que x=0 y x=2 son las dos asíntotas verticales de f(x). Efectivamente, se puede comprobar que:
En la siguiente gráfica tienes un esbozo de la situación.
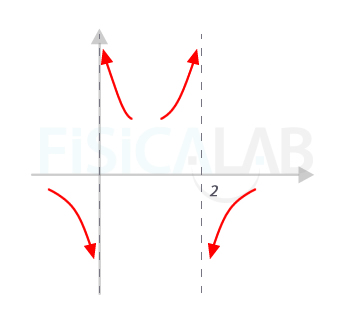
Encontrarás asíntotas verticales en aquellas funciones racionales que den lugar a una indeterminación del tipo k/0
Cálculo en funciones logarítmicas
Las funciones logarítmicas tienen una asíntota vertical en el punto en que se anula el argumento. Así, por ejemplo:
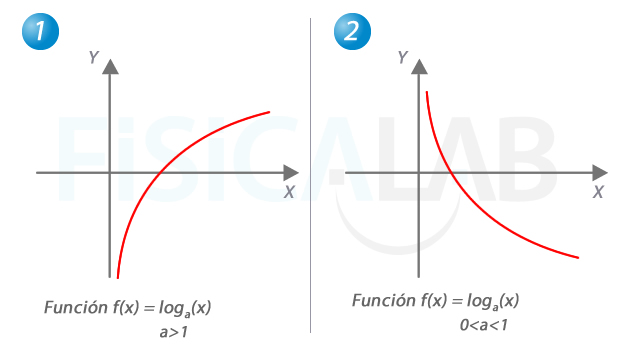
Asíntotas en funciones logarítmicas
Las funciones logarítmicas tienen una asíntota vertical en los puntos en que se anula el argumento (x=0 en el caso de las dos gráficas de la figura). En 1, forma de las funciones logarítmicas cuando la base es mayor que 1. A la derecha, el caso de las funciones logarítmicas con base entre 0 y 1.
Funciones trigonométricas
Las funciones trigonométricas seno y coseno no tienen asíntotas de ningún tipo. Las funciones que se forman a partir de estas, tangente, cosecante, secante y cotangente, tienen asíntotas verticales cuando se anula el denominador. Recuerda que:
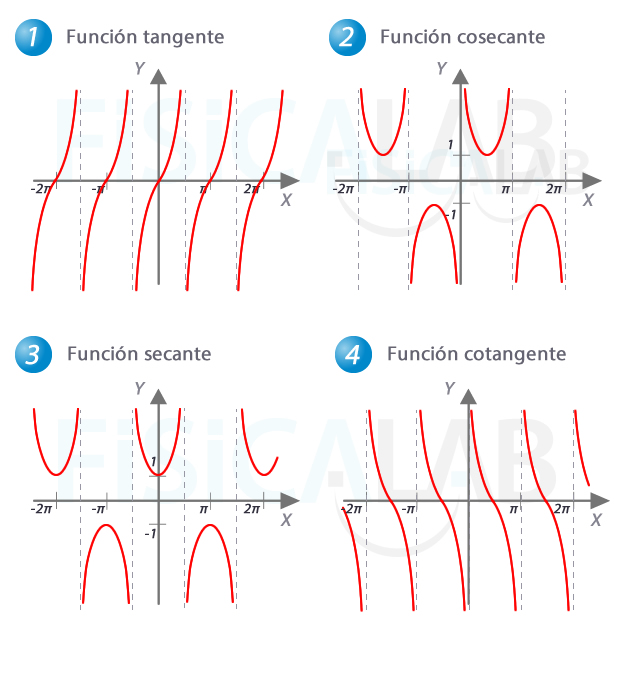
Asíntotas en funciones trigonométricas
Las funciones trigonométricas tienen asíntotas verticales en aquellos puntos en que se anula el denominador, lo cual ocurre de manera periódica en las funciones tangente de x (1), cosecante de x (2), secante de x (3) y cotangente de x (4).
Asíntotas horizontales
Decimos que la recta y=k es una asíntota horizontal de la función f(x) cuando se cumple:
Donde:
- k: Es el valor real, por ejemplo 3, 0 ó -1, al que se aproxima la función (su coordenada y) cuando la x se hace infinitamente grande, por la derecha (x→∞) o por la izquierda (x→-∞)
- f(x): Es la función que presenta la asíntota
Por tanto para a saber si una función presenta asíntotas horizontales, basta calcular los límites anteriores, en infinito y menos infinito, y ver si alguno da un valor real concreto.
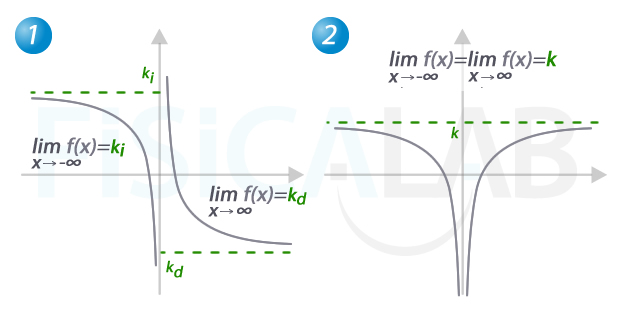
Asíntotas horizontales
Gráficamente, las asíntotas horizontales se distinguen porque cuando la x se hace infinitamente grande (por la derecha o por la izquierda), la función se aproxima a un valor concreto. Según consideremos el límite en +∞ o -∞, decimos que la asíntota horizontal se presenta por la derecha o por la izquierda de la función respectivamente. Por tanto, una función puede tener ninguna asíntota horizonte, una, como en el caso de la figura 1, o dos, como en el caso de la figura 2.
Cálculo en funciones racionales
En este caso, siendo f(x)=P(x)/Q(x) una función racional, resulta inmediato el cálculo de
- Si grado P(x) < grado Q(x), y=0 será asíntota horizontal.
- Si grado P(x) = grado Q(x), el cociente entre los términos de mayor grado del numerador y del denominador es la asíntota horizontal
Ejemplo
Para calcular las asíntotas horizontales de
Por tanto, como es un valor concreto, y=1 es una asíntota horizontal. Ahora, la izquierda:
Así, por la izquierda la asíntota horizontal también es y=1.
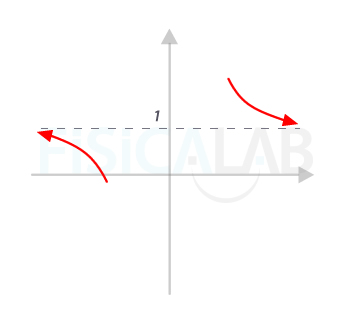
Esbozo de asíntotas horizontales
En la figura, el esbozo de las asíntotas horizontales del ejemplo. Observa que, mientras la rama izquierda se acerca a la asíntota y=1 desde abajo, la derecha lo hace desde arriba. Para distinguir un caso del otro damos a la x valores muy grandes, positivos y negativos respectivamente, y comprobamos si el valor de la función es ligeramente superior o inferior al de la asíntota. Si es inferior, la función se acerca desde abajo. Si es superior lo hace desde arriba.
Cuando, al calcular los límites en el infinito de la función, obtenemos ±∞, en lugar de k, nos encontramos ante una asíntota oblicua o ante una rama parabólica.
Cálculo en funciones exponenciales
Las funciones exponenciales tienen una asíntota horizontal en menos infinito o en infinito según la base sea mayor que uno o esté entre 0 y 1 respectivamente. Así, por ejemplo:
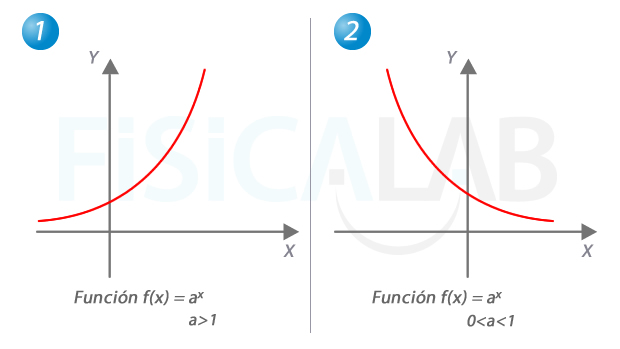
Asíntotas en funciones horizontales
Las funciones exponenciales tienen una asíntota horizontal en menos infinito o en infinito según su base sea mayor que uno (función izquierda) o esté entre 0 y 1 (función derecha).
Asíntotas oblicuas
Decimos que la recta y=m·x+n es una asíntota oblicua de la función f(x) cuando se cumple:
Donde:
- x→∞: Puede ser también x→-∞
- m: Es la pendiente de la asíntota, y por tanto debe ser un valor real distinto de cero, ya que si fuera cero nos encontraríamos ante una recta horizontal
- n: Es el otro parámetro que define la recta, su ordenada en el origen. Esta vez si puede ser 0, para el caso de las asíntotas que pasan por el origen (0,0)
- f(x): Es la función que presenta la asíntota
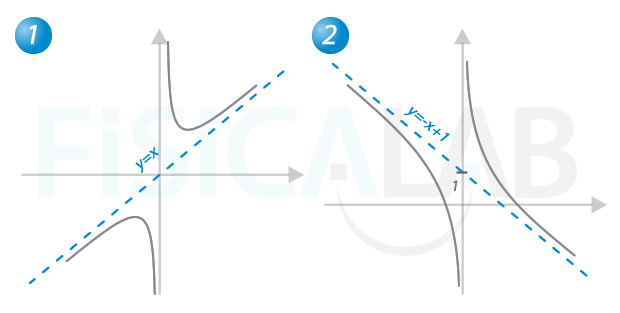
Asíntotas oblicuas
Gráficamente, las asíntotas oblicuas se distinguen porque cuando la x se hace infinitamente grande (por la derecha o por la izquierda), la función se aproxima a una recta con cierta pendiente m. A la izquierda, en 1, a medida que crecen los valores de x, los correspondientes valores de y=f(x) se aproximan a la recta y=x (m=1, n=0). A la derecha, a medida que creen los valores de x, la función se aproxima a y=-x+1 (m=-1, n=1).
Cálculo en funciones racionales
Cuando la función es racional, f(x)=P(x)/Q(x), se producen asíntotas oblicuas siempre que grado P(x) - grado Q(x) = 1. Si es así, realizaremos la división de P(x) entre Q(x): El cociente de la misma, en la forma m·x+n, es la asíntota oblicua.
Justificación
Recordamos que, según la "prueba de la división", el dividendo, P(x), es igual a cociente, C(x), por divisor, Q(x), más el resto, R(x), con lo que:
El cociente R(x)/Q(x), en rojo, tiende a ser cada vez más pequeño para valores altos de x (ya que el grado del resto R(x) será menor al del divisor Q(x), con lo que la función P(x)/Q(x) se comportará de manera cada vez más parecida a la del cociente C(x), que es un polinomio de grado 1, es decir, la recta oblicua que constituye la asíntota de la función.
Ejemplo
Podemos buscar las asíntotas oblicuas de
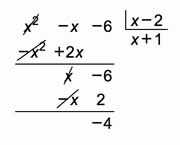
De manera que la asíntota oblicua es directamente y=x+1.
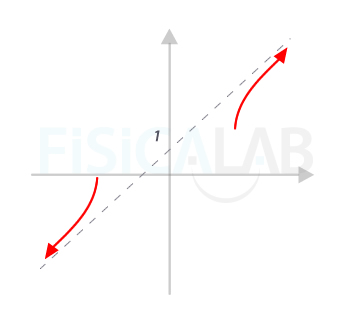
Esbozo de asíntotas oblícuas
En la figura, el esbozo de las asíntotas oblicuas del ejemplo. Observa que, mientras la rama izquierda se acerca a la asíntota y=x+1 desde arriba, la derecha lo hace desde abajo. Al igual que sucedía con las asíntotas horizontales, para distinguir un caso del otro, damos a la x valores muy grandes, positivos y negativos respectivamente, y comprobamos si el valor de la función es ligeramente superior o inferior al de la asíntota. Si es inferior, la función se acerca desde abajo. Si es superior lo hace desde arriba.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
