Límite de una Función en el Infinito

De manera intuitiva, el límite de una función real en el infinito (o en el menos infinito) es el valor al que se aproxima la función (es decir, su coordenada y) a medida que la coordenada x se hace "más y más grande". En la siguiente imagen queda recogido el concepto y la notación que se suele utilizar:

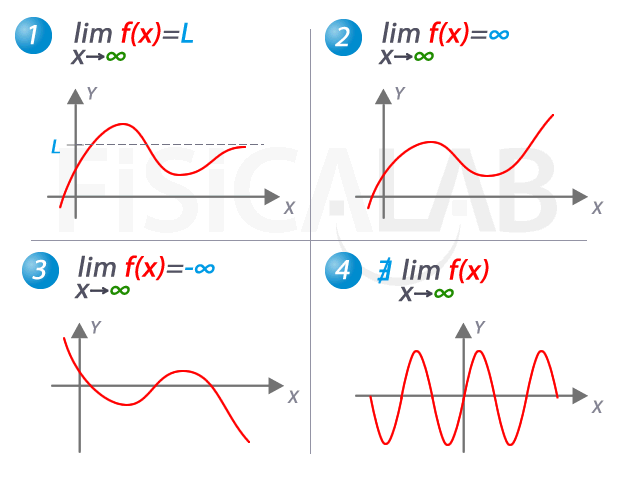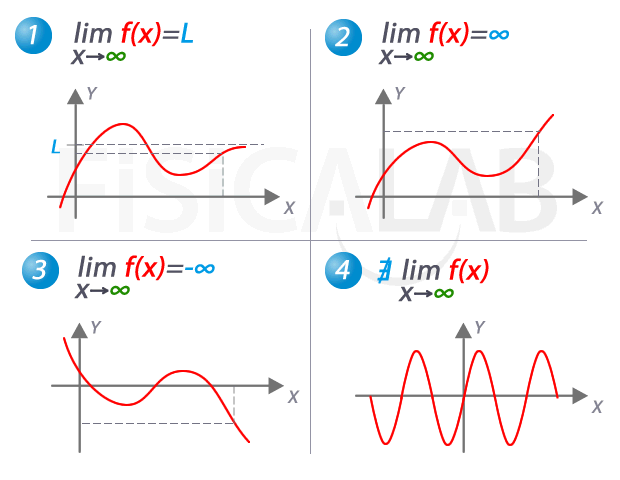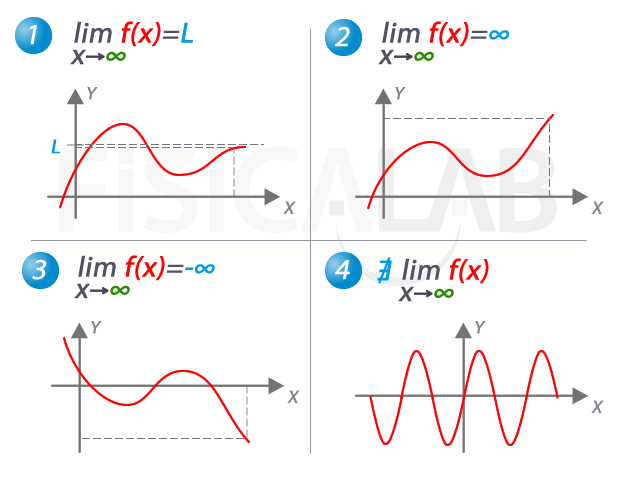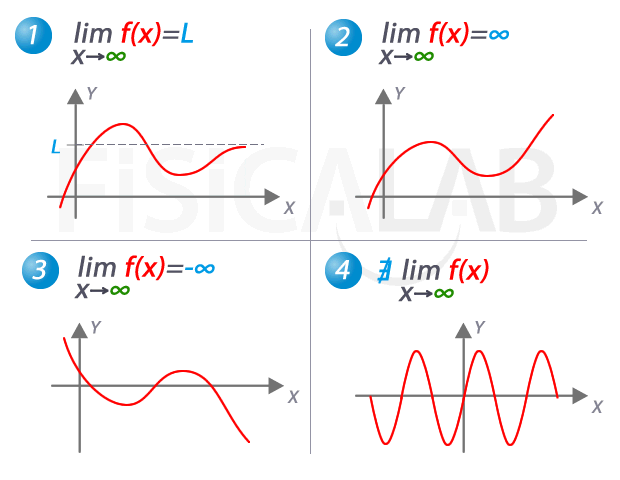
Límite cuando x tiende a ∞

En la imagen, los 4 posibles comportamientos de la función cuando el valor de x crece indefinidamente (decimos, cuando x tiende a ∞). En 1, la función se aproxima a L, por tanto ese es el valor del límite. En 2, la función se va al infinito y en 3 se va a menos infinito. En 4, no existe el límite ya que la función es periódica y no se aproxima a ningún valor concreto.

En este apartado vamos a darte, a partir de esta idea intuitiva, unas definiciones más formales para cada uno de estos casos. Lo haremos en los siguientes puntos:

• Aproximaciones al infinito
• Valor finito del límite
• Valor infinito del límite
• Valor menos infinito del límite

Si lo que deseas es aprender a calcular el valor de dicho límite, y ya tienes claro el concepto, visita el apartado enlazado. Por el contrario, si lo que deseas es conocer el concepto de límite de una función en un punto, hazlo en ese otro.

Aproximaciones sucesivas al infinito

Ya hemos hablado en apartados anteriores de la estrecha relación que guardan los límites con la idea de aproximarnos sucesivamente a un valor concreto. En este caso, y estrictamente hablando, el infinito no es un valor, sino más bien una idea. ¿Qué significa por tanto que x→∞?. Veámoslo con un ejemplo concreto:

$$f\left(x\right)=\frac{1}{x}$$

Vamos a darle valores cada vez mayores a la x:

Como puedes intuir, a medida que nos acercamos al infinito, el valor de la función se aproxima a cero. Es por eso que decimos que $\underset{x\to \infty }{\lim }\frac{1}{x}=0$. Sin embargo, esto no significa que $\frac{1}{\infty }=0$ (en realidad, no sabemos cuánto vale esa expresión). Vemos de nuevo, que el límite es un concepto dinámico, que tiene que ver con el aproximarse a ciertos valores, frente al valor de una función en un punto, que es un concepto estático.

Nota: De manera análoga, podemos estudiar lo que le sucede a la función cuando la x se hace muy negativa (diremos muy pequeña, aunque el lenguaje puede engañarte: ten presente que no nos referimos a que se aproxime a 0).

Por tanto, a medida que nos acercamos al menos infinito, la función también se aproxima a 0.

Valor finito

El límite de una función cuando x tiende a infinito es L si podemos conseguir que f(x) esté tan próximo a L como queramos, dándole a x valores suficientemente grandes.

Para hacer la definición formal, nos valemos de la idea de entorno. Recuerda que un entorno de centro a y radio r es un intervalo abierto de valores próximos a dicho número real y que lo contiene, es decir, $E\left(a,r\right) =\hspace{0.17em}\left(a-r, a+r\right)$, que también se puede expresar como aquellos valores x que cumplen |x-a|<r.

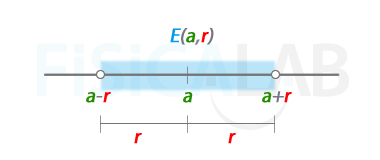
Entorno de centro a y radio r

Representación gráfica de un entorno con centro a y radio r. Es un intervalo abierto en el que la distancia entre el centro a y los extremos es r.

Formalmente:

De manera análoga, podemos decir que el límite de una función cuando x tiende a menos infinito es L si podemos conseguir que f(x) esté tan próximo a L como queramos, dándole a x valores suficientemente pequeños.

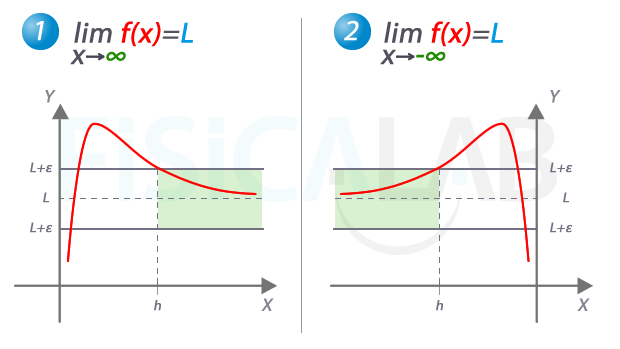
Valor finito en límite cuando x tiende a ∞ o a -∞

Elementos de la definición cuando x tiende a ∞ (a la izquierda) o a -∞ (a la derecha). En el primer caso, a partir de h, se cumple la condición de que las imágenes están siempre en el entorno de L (esto es lo que significa que $\left|f\left(x\right)-L\right|<\epsilon$). Como la función se aproxima a L a medida que x aumenta, aunque fijemos una ε muy pequeña, siempre se puede encontrar un h que cumpla la condición señalada. En el segundo caso, la condición de que las imágenes están siempre en el entorno de L se cumple hasta h.

En ambos casos, decimos que la recta y=L es una asíntota horizontal de la función.

Valor infinito

El límite de una función cuando x tiende a infinito es infinito si podemos conseguir que f(x) sea tan grande como queramos, sin más que dar a x valores suficientemente grandes. Formalmente:

Análogamente, el límite de una función cuando x tiende a menos infinito es infinito si podemos conseguir que f(x) sea tan grande como queramos, sin más que dar a x valores suficientemente pequeños. Formalmente:

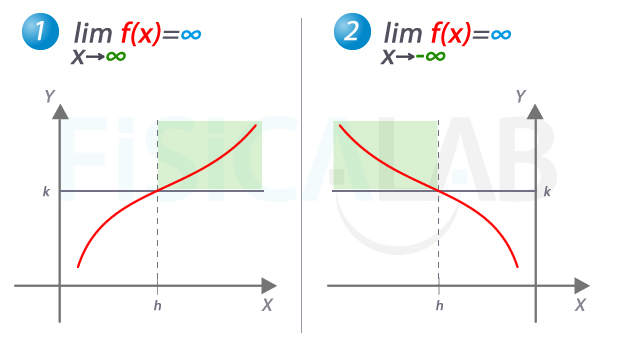
Valor infinito en límite cuando x tiende a ∞ o a -∞

Elementos de la definición cuando x tiende a infinito (izquierda) o a menos infinito (derecha). En el primer caso, a partir de h las imágenes de x son siempre mayores que k. Como la función crece indefinidamente, siempre se puede encontrar un valor h que cumpla esta condición independientemente de lo grande que sea k. A la derecha, el caso análogo, en el que las imágenes de x son siempre mayores que k hasta un valor determinado, que es el que llamamos h.

Valor menos infinito

El límite de una función cuando x tiende a infinito es menos infinito si podemos conseguir que f(x) sea tan pequeña como queramos, sin más que dar a x valores suficientemente grandes. Formalmente:

Así mismo, el límite de una función cuando x tiende a menos infinito es menos infinito si podemos conseguir que f(x) sea tan pequeña como queramos, sin más que dar a x valores suficientemente pequeños. Formalmente:

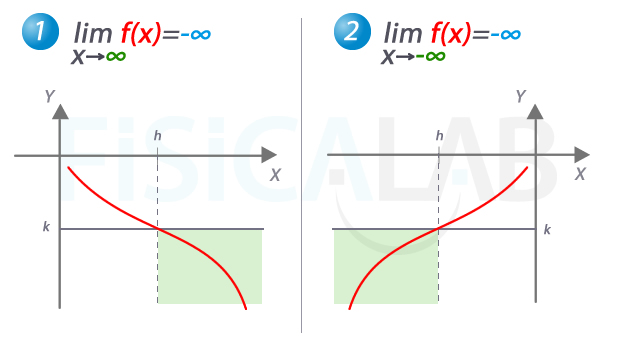
Valor menos infinito en límite cuando x tiende a ∞ o a -∞

Elementos de la definición cuando x tiende a infinito (izquierda) o a menos infinito (derecha). En el primer caso, a partir de h las imágenes de x son menores que k. Como la función decrece indefinidamente, siempre se puede encontrar un valor h que cumpla esta condición independientemente de lo pequeña que sea k. A la derecha, el caso análogo, en el que las imágenes de x son siempre menores que k hasta un valor determinado, que es el que llamamos h.