Función Implícita y su Derivada

Por ejemplo, la igualdad $x^2-y=0$, correspondiente a y=x², es una función implícita. También $y^3-5x^2+3x{y}^2+12=0$.

Gráfica de una función implícita

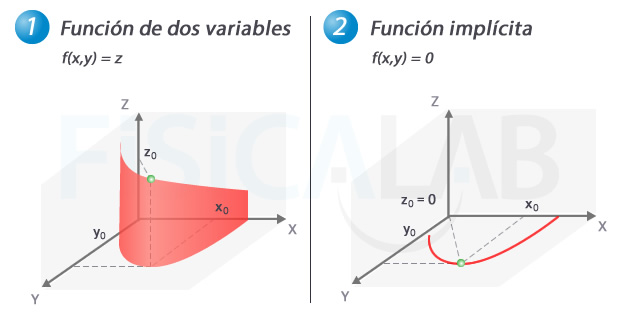
Gráficamente, se pude considerar una función implícita como un caso particular de una función de dos variables f(x,y)=z en el que z siempre vale 0. Observa la gráfica en 1. Se trata de una función de dos variables (x e y). En ella se asigna un número real z₀ (una altura de la curva) a cada punto (x₀, y₀) del plano OXY que pertenezca al dominio. Como se aprecia en 2, si forzamos z=0 obtendríamos una función "pegada" al plano OXY, es decir, una función de una sola variable que quedaría representada dos dimensiones.

Derivada

La derivación implícita es la técnica que nos permite obtener la derivada de la función implícita. Se trata simplemente de aplicar la regla de la cadena, considerando y como una función que depende de x. Veámoslo con la función de nuestro ejemplo anterior $y^3-5x^2+3x{y}^2+12=0$. Plantearemos cada sumando de más sencillo a más complejo:

• $D\left(12\right)=0$

• $D\left(5x^2\right)=10x$

• $D\left(y^3\right)=3y^2·y\text{'}$

  Como decíamos, hemos considerado y una función que depende de x y aplicado la regla de la cadena

• $D\left(3x{y}^2\right)=3\left(y^2+x·2yy\text{'}\right)$

  En este caso hemos considerado un producto de funciones Así, recuerda que D(u·v)=u'v+uv'. Partimos de la constante 3 que multiplica la primera 'función' u=x, y la segunda v=y².

Con lo que podemos escribir:

$$3y^{2}y\text{'}-10x+3y^2+6xyy\text{'}=0\Rightarrow y\text{'}=\frac{10x-3y^2}{3y^2+6xy}$$

Así, la derivada también queda expresada de forma implícita. Si quisiéramos obtener el valor concreto de dicha derivada en un punto (x₀,y₀) tendríamos que conocer el valor de la función en dicho punto. Por ejemplo, sabiendo que la curva pasa por el punto $\left(0, \sqrt[3]{-12}\right)$, la derivada en dicho punto quedaría:

$$y\text{'}\left(0, \sqrt[3]{-12}\right)=\frac{-3{\left(\sqrt[3]{-12}\right)}^2}{3{\left(\sqrt[3]{-12}\right)}^2}=-1$$