Tasa de Variación Media
La tasa de variación media de una función en un intervalo nos permite estudiar el cambio que experimenta dicha función en el intervalo. En este apartado la vamos a estudiar a través de los siguientes puntos:
La tasa de variación media es el primer paso para que puedas empezar a entender qué es una derivada.
¿Empezamos?
Concepto
Observa la siguiente imagen:
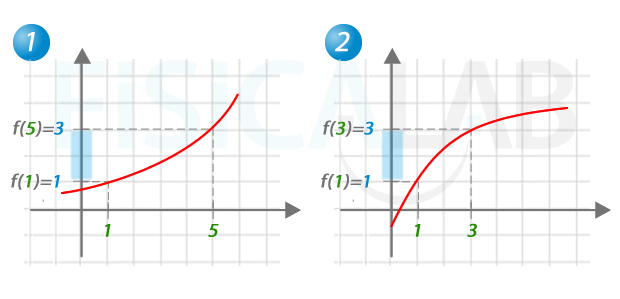
Tasa de variación de una función
La tasa de variación de una función en un intervalo [a,b] nos dice cuánto cambia la función en dicho intervalo. En 1, la tasa de variación de la función en el intervalo [1,5] es 2, porque f(b)-f(a)=f(5)-f(1)=3-1=2. En 2, la tasa de variación en el intervalo [1,3] también es 2: f(b)-f(a)=f(3)-f(1)=3-1=2.
Como ves, ambas funciones crecen lo mismo, pero el intervalo que le lleva a la primera alcanzar esa variación es de 4 unidades (pues el intervalo [1,5] "mide" 4 unidades), mientras que la segunda alcanza esa variación en tan solo 2 (pues el intervalo [1,3] "mide" 2 unidades). Así pues, para caracterizar el comportamiento de la función en el intervalo podemos hacer uso de otra expresión más precisa: la tasa de variación media.
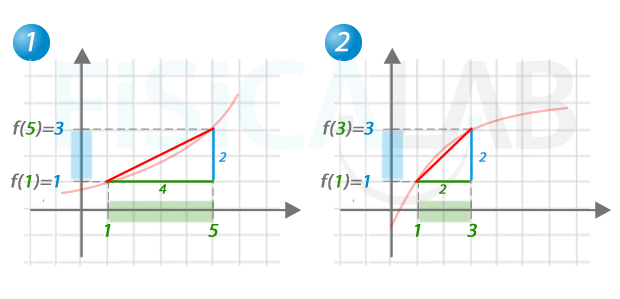
Tasa de variación media de una función
La tasa de variación media de una función en un intervalo [a,b] nos dice cuánto cambia la función de media en dicho intervalo. Para obtenerla hay que considerar tanto el cambio que se produce en el eje y, en azul, como el cambio que se produce en el eje x, en verde.
Expresión
Como puedes suponer, para obtener la tasa de variación media (T.V.M.) en un intervalo [a, b] dividimos la variación de la función (es decir, su tasa de variación) entre la variación de x:
La variación que se produce en y es, como ya hemos visto, f(b)-f(a). La variación que se produce en x es directamente b-a. Más formalmente:
Definimos la tasa de variación media de una función f(x) en un intervalo [a, b] como:
La expresión anterior está dada en función de los extremos del intervalo (a y b). En ocasiones es habitual expresar un intervalo como [a, a+h], siendo h la longitud del mismo. En este caso:
La tasa de variación media también puede ser expresada como:
Comprobación
Si consideramos b=a+h nos queda:
Cuando la tasa de variación media en un intervalo es positiva, significa que la función crece en dicho intervalo. Si es negativa, la función decrece.
Representación e Interpretación geométrica
Geométricamente, la tasa de variación media es la pendiente de la recta que pasa por los puntos (a,f(a)) y (b, f(b)).
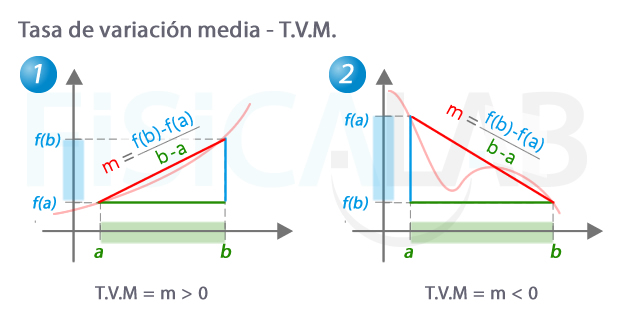
Representación gráfica de la tasa de variación media
En rojo, la recta que pasa por los puntos (a,f(a)) y (b, f(b)). Se denomina recta secante (recta que corta). El valor de su pendiente, m, es, precisamente, la tasa de variación media. Observa que, en 1, la función es creciente y la T.V.M. > 0, pues f(b)>f(a). En cambio, en 2, la función es decreciente y la T.V.M. < 0 pues f(b)<f(a). Observa que, en este último caso, hay subintervalos de [a,b] en los que la función es creciente, aunque globalmente es decreciente, de ahí que la tasa de variación media sea negativa.
Justificación
Conocida la ecuación de una recta en forma explícita, y=m·x+y0, que pasa por los puntos (x,y) = (a,f(a)) y (x,y) = (b,f(b)), podemos escribir:
Como ves, calculando m, la pendiente de la recta que pasa por los puntos considerados, obtenemos el mismo valor de la T.V.M.
Ejemplos en física
La tasa de variación media es una magnitud muy utilizada en ciencias para estudiar como cambian ciertas magnitudes respecto a otras. Por ejemplo, para estudiar como varía la velocidad en un intervalo de tiempo estudiamos su velocidad media, que no es más que la tasa de variación media de la posición respecto al tiempo. Cuando la velocidad media es grande, la posición varía mucho para una variación de tiempo dada.
Otro ejemplo sería la segunda ley de Newton. Así, para estudiar la fuerza aplicada a un cuerpo en un intervalo de tiempo estudiamos la tasa de variación media del momento lineal respecto al tiempo en ese intervalo. Cuando la fuerza aplicada en el intervalo es alta, el momento lineal varía mucho en ese intervalo de tiempo. Cuando la fuerza aplicada es pequeña, la variación del momento lineal también es pequeña. Te invitamos a que navegues los contenidos de la web para encontrar fórmulas que puedas interpretar bajo este punto de vista.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
