Derivada de la Función Inversa
Conocida una función f, y su inversa f-1, es posible obtener la derivada de esta última a partir de la siguiente expresión:
Nota: Visita el apartado de funciones inversas para recordar cuándo es posible obtenerlas y cómo se calculan.
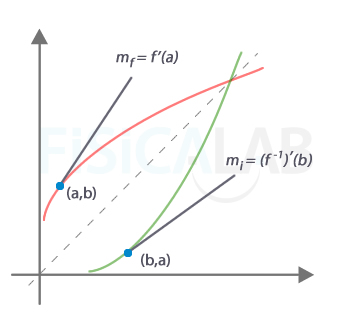
Interpretación gráfica
En rojo, una función cualquiera f. Su inversa f-1, representada en verde, es simétrica respecto a la bisectriz del primer cuadrante. Por tanto, se cumple que la pendiente de la recta tangente de la función original en un punto arbitrario (a,b), mf, y de la función recíproca en el punto recíproco (b,a), mi, guardan la relación mi=1/mf. Con esto nos queda que:
Por otro lado, sabemos que (a,b)=(a,f(a)) es simétrico con (b,a)=(b,f-1(b)), es decir, a=f-1(b). De esta manera se puede escribir:
Ejemplo
Sea
Ten presente que siempre puedes calcular la derivada de la función recíproca aplicando las reglas de derivación habituales, como si se tratara de cualquier otra función.
Demostración
La composición de una función con su inversa resulta en la función identidad:
Derivando ambos miembros obtenemos:
Donde hemos aplicado la regla de la cadena para derivar la función compuesta f[f-1].
El uso de la expresión anterior es de particular interés para el cálculo, por ejemplo, de la derivada de las funciones trigonométricas arcoseno, arcocoseno y arcotangente, cuyas recíprocas, el seno, el coseno y la tangente, tienen derivadas que se pueden obtener fácilmente aplicando la definición.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
