Cómo Representar una Función Cualquiera
De una manera intuitiva, representar una función f(x) consiste en ir dando valores a la variable independiente x e ir obteniendo los correspondientes valores de la función y=f(x). Dicho de otro modo, se trata de buscar todos los (x, y)= (x,f(x)) posibles. Este método, consistente en elaborar una tabla de valores, es el que hemos empleado en niveles anteriores, por ejemplo en este ejercicio sobre la representación gráfica.
En este nivel esbozaremos la forma de la gráfica a partir de nuestros conocimientos en límites y derivadas, y emplearemos la tabla de valores sólo como una ayuda adicional cuando queramos ser más precisos en algunos valores de x.
Pasos
Te proponemos que sigas los siguientes pasos, y recojas la información en una tabla:
-
Estudia el dominio de la función. Esto nos va a permitir saber en qué valores de x existe la función y en cuáles no debemos dibujar nada
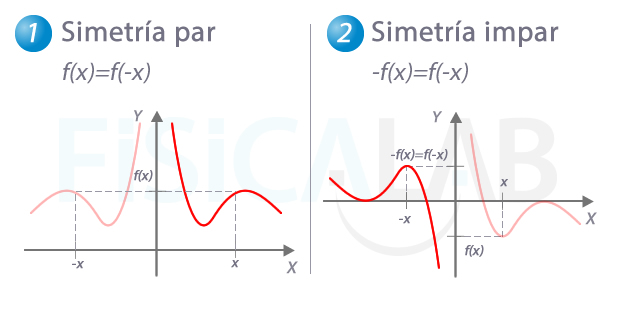
Estudia la simetría de la función. Si la función es simétrica te bastará representar una mitad, pues la otra podrás obtenerla "reflejando" la primera
Estudia la periodicidad de la función. Las funciones trigonométricas pueden ser simétricas. Si la función es periódica te bastará representar un solo periodo y "replicarlo"
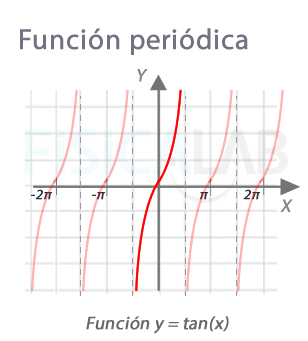
Concepto de función periódica
La tangente de x es un ejemplo de función periódica. En estos casos podemos representar un sólo periodo, por ejemplo entre -π/2 y π/2, y replicar en el resto.
Estudia los puntos de corte con los ejes
Puntos de corte con el eje y: Se obtienen haciendo x=0 y despejando y
Puntos de corte con el eje x: Se obtienen haciendo y=0 y despejando x. En ocasiones es posible que no sepas resolver la ecuación obtenida al hacer y=f(x)=0. Recuerda que con el teorema de Bolzano siempre puedes aproximar los puntos de corte con el eje x, como veíamos en este ejemplo
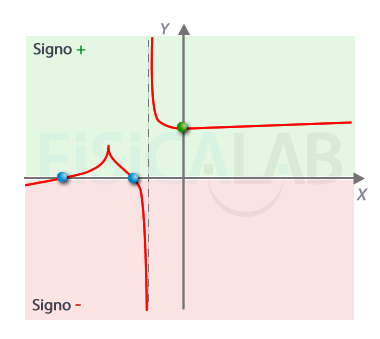
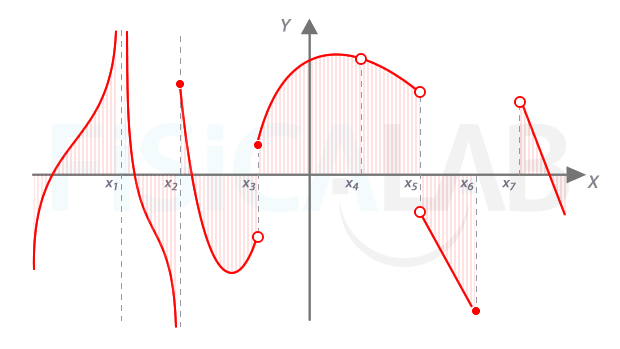
Signos de la fución y cortes con los ejes
Una función puede tener varios cortes con el eje x (en azul), pero como máximo solo tendrá un corte con el eje y (en verde). En los puntos de corte con el eje x, también llamado de abscisas, la función puede cambiar su signo (aunque no necesariamente).Observa que en el caso de que el corte se produzca en el (0,0), se trata de un corte con el eje x e y a la vez.
Para ralizar los pasos del 1 al 4 anteriores te basta la expresión analítica de la función y no es necesario recurrir a límites ni derivadas.
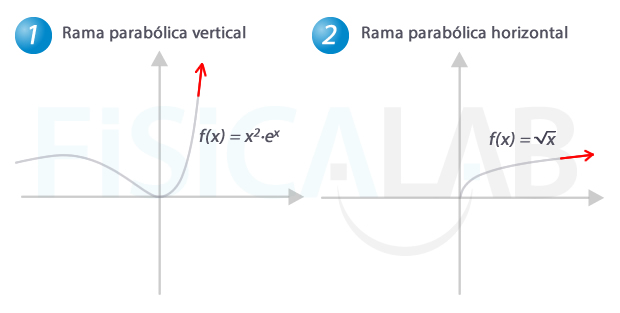
Estudia las ramas infinitas de la función esto es:
Sus asíntotas
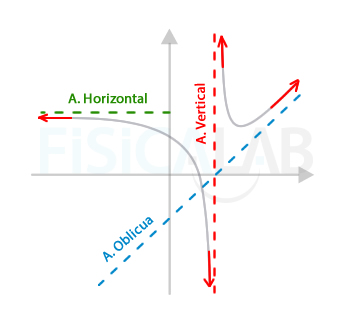
Concepto de asíntotas
Recuerda, una asíntota es una recta a la cual la función se aproxima indefinidamente, pero nunca la toca. Es importante conocer las asíntotas de la función para poder esbozarla.
De una manera práctica, para estudiar qué ocurre cuando x→∞ puedes seguir los siguientes pasos:
Estudia
Si no existe, ya has concluido
Existe asíntota horizontal si
Debes continuar con el paso 2 si
Estuida
Si no existe, no hay asíntota oblicua, y ya has concluido
Si
Si
Estudia
Si
Si no existe no hay ramas infinitas
Puedes proceder análogamente cuando x→-∞.
- Estudiamos la monotonía y los extremos de la función, a través de la primera derivada f'(x)
- Estudiamos la curvatura de la función, a través de la segunda derivada f''(x)
Con toda la información aterior recogida en una tabla ya puedes realizar un esbozo bastante aproximado de la función. Si deseas mayor precisión en determinados entornos de x, utiliza una tabla de valores.
Estos 7 pasos pueden ser considerados un método genérico, pero no siempre es neceario completar todos ellos. Así por ejemplo, la representación de funciones polinómicas se simplifica bastante. Visita los apartados del tema de funciones habituales para profundizar en la representación de funciones según su tipo.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.