Componentes Intrínsecas de la Aceleración

En Física decimos que un cuerpo tiene aceleración cuando se produce un cambio del vector velocidad, ya sea en módulo o dirección. En apartados anteriores hemos visto que si este cambio se produce en un intervalo de tiempo se habla de aceleración media en el intervalo y si se produce en un instante de tiempo se habla de aceleración instantánea. En este apartado vamos a estudiar las componentes de la aceleración atendiendo al efecto que producen en la velocidad.

Concepto de Componentes Intrínsecas

En apartados anteriores hemos definido la aceleración como el cambio del vector velocidad con el tiempo. Hemos dicho que el vector velocidad puede cambiar en módulo o en dirección. Por tanto aparecen claramente dos efectos de la aceleración:

La variación del módulo de la velocidad
La variación de la dirección de la velocidad

Para poder estudiar claramente estos efectos, utilizamos un sistema de referencia intrínseco en cada punto de la trayectoria, tal y como se puede ver en la figura.

el sistema de referencia intrínseco se establece para cada punto de la trayectoria. Uno de sus ejes es tangente en ese punto y el sentido positivo es el que corresponde con el vector velocidad. El otro es un eje perpendicular y su sentido positivo se dirige hacia el centro de curvatura.

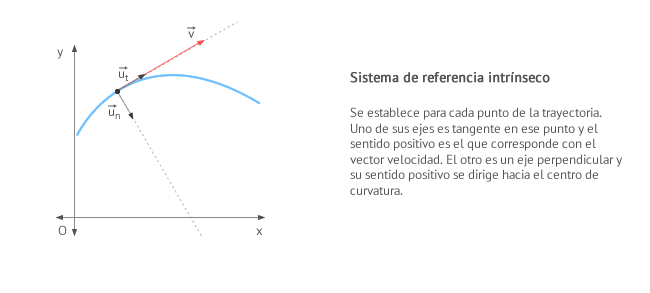
Se define el sistema de referencia propio o intrínseco para cada punto de la trayectoria como un sistema de coordenadas formado por dos ejes:

Eje tangente: Su dirección es tangente a la trayectoria y el sentido positivo será el de la velocidad en ese punto. Se define por el vector unitario ${\vec{u}}_{t}$
Eje normal: Su dirección es perpendicular a la trayectoria y el sentido positivo será el que se dirige al centro de curvatura de la trayectoria. Se define por el vector unitario ${\vec{u}}_{n}$

Este sistema de referencia es el que se usa para "observar" los cambios del vector velocidad en módulo y dirección.

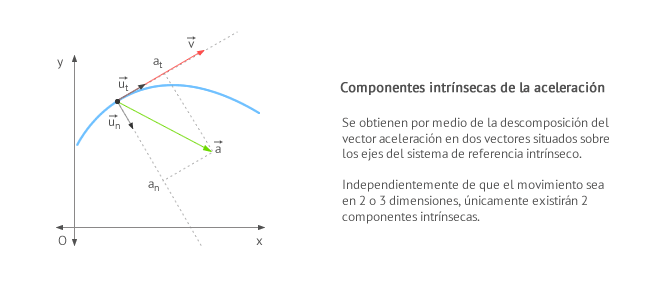
Se definen las componentes intrínsecas de la aceleración como la descomposición del vector aceleración en los ejes intrínsecos.

A la componente que se proyecta sobre el eje tangente se le llama componente tangencial y es la responsable del cambio del módulo de la velocidad.
A la que se proyecta sobre el eje normal se le llama componente normal o componente centrípeta y es la responsable de la dirección de la velocidad.

Se puede expresar la aceleración en función de sus componentes en la forma:

\vec{a} = {\vec{a}}_{t} + {\vec{a}}_{n} = a_{t} {\vec{u}}_{t} + a_{n} {\vec{u}}_{n}

Donde:

$\vec{a}$ : Es el vector aceleración en un punto determinado
${\vec{a}}_{t}$ , ${\vec{a}}_{n}$ , $a_{t}$ , $a_{n}$ : Son los vectores aceleración tangencial y normal y sus respectivos módulos
${\vec{u}}_{t}$ , ${\vec{u}}_{n}$ : Son los vectores unitarios en las direcciones del eje tangente y del eje normal respectivamente

Como puedes observar en la siguiente figura, dado que los ejes son perpendiculares entre sí, el módulo de la aceleración puede calcularse como

|\vec{a}| = \sqrt{a_{t}^{2} + a_{n}^{2}}

Es importante que te des cuenta que, independientemente de si el movimiento se está realizando en dos o en tres dimensiones, el módulo del vector aceleración descrito en función de sus componentes intrínsecas tiene dos variables a lo sumo: la de la aceleración tangencial que se corresponde al eje tangente y la de la aceleración normal correspondiente al eje normal .

Componentes Intrínsecas de la aceleración. Se obtienen por medio de la descomposición del vector aceleración en dos vectores situados sobre los ejes del sistema de referencia intrínseco. Independientemente de que el movimiento sea en 2 o 3 dimensiones, únicamente existirán 2 componentes intrínsecas.

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:

Intermedio

Aceleración

Otros idiomas:

Inglés

Navegación

Componentes Intrínsecas de la Aceleración

Compartir en...

Síguenos en...

Concepto de Componentes Intrínsecas

Y ahora... ¡Ponte a prueba!

José L. Fernández

Apartados relacionados

Otros idiomas:

Navegación