Representación de Números Complejos en Forma Binómica
Si haces un poco de memoria recordarás que los números reales se representan en una recta que recibe el nombre de recta real. Si el conjunto de los números complejos contiene a los números reales, ¿Cómo representar gráficamente estos números?
Representación de los número reales
Los números reales se representan por medio de una recta que recibe el nombre de recta real.
El matemático y físico alemán Carl Friedrich Gauss (1777-1855) fué el primero en realizar una representación de los números complejos estableciendo que estos no se podían dibujar en una recta, como los reales, si no que se debían representar en un plano que denominó plano complejo. De esta forma, la parte real se puede representar en el eje de abcisas, también denominado eje real y la parte imaginaria en el eje de ordenadas, también llamado eje imaginario.
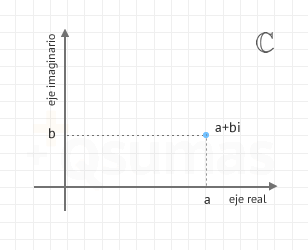
Representación de los números complejos
A cada número complejo a+bi le corresponde un punto en un plano. Dicho punto posee las coordenadas (a,b).
Utilizando estos criterios cada número a + bi queda representado por un punto P cuyas coordenadas son (a,b). Dicho punto P recibe el nombre de afijo, de tal forma que a cada número complejo le corresponde un afijo, y a cada afijo un número complejo.
Características de los números complejos en forma binómica
Si observamos detenidamente la forma de un número complejo cualquiera a + bi podemos deducir las siguientes características:
-
Si b = 0, el número complejo es básicamente el número real a. Esto pone de manifiesto lo que comentabamos en apartados anteriores: los números reales son un subconjunto de los números complejos (ℝ⊂ℂ) y la representación de estos últimos es compatible con la de los reales ya que en este caso cualquier número real se encontrará sobre el eje real (la recta real).
- Si a = 0, el número complejo posee sólo parte imaginaria y recibe el nombre de número imaginario puro. Se representan con un punto situado directamente sobre el eje real.
- Si a = 0 y b = 0, el número se denomina número complejo cero y al representarse su afijo se encuentra sobre el origen de coordenada.
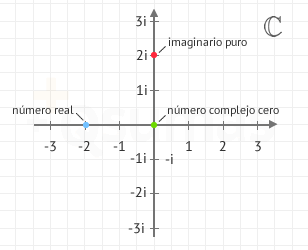
Los números reales son un subconjunto de los números complejos
En la figura se muestra el número real -2 que se representa como un punto sobre la recta real, el número imaginario puro 2i que se representa como un punto sobre el eje imaginario y el cero que se localiza en el origen de coordenadas.
Observa que el -2 a demás de ser un número real es también un número complejo. Esto es debido a que los números reales son un subconjunto de los complejos.
- Se dice que dos números complejos, a+bi y c+di, son iguales si sus partes real e imaginaria son iguales, es decir, si se cumple que a=c y b=d.
- Si denominados
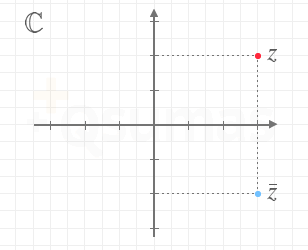
Número complejo conjugado
El conjugado (
- Dado un número complejo
Número complejo opuesto
El opuesto (-Z) de un número complejo cualquiera (Z) posee su parte real e imaginaria con signo opuesto. Gráficamente ambos números se representan simétricos respecto al origen de coordenadas.
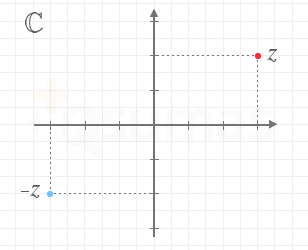
Número complejo opuesto
El opuesto (-Z) de un número complejo cualquiera (Z) posee su parte real e imaginaria con signo opuesto. Gráficamente ambos números se representan simétricos respecto al origen de coordenadas.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
