Representación de Números Complejos en Forma Polar
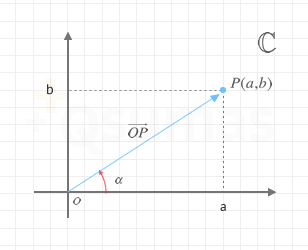
Cada número complejo en forma binómica a + bi se representa como un punto P(a,b) en el plano complejo. Como podrás suponer esta no es la única forma de representarlos. De hecho, otra forma alternativa de representación consiste en utilizar el vector que se define entre el origen de coordenadas y el punto P (denominado afijo del número complejo). De esta forma cada número complejo en vez de venir determinado únicamente por los valores a y b puede venir dado por la longitud (o módulo) del vector
Representación de números complejos en forma polar
Cualquier número complejo a+bi está representado por su afijo en las coordenadas (a,b). Dicho punto puede venir dado igualmente por la longitud del vector que une el origen con el afijo (
Módulo de un número complejo
Se llama módulo, longitud o valor absoluto de un número complejo z = a + bi, representado como m, |z|, |
Argumento de un número complejo
El argumento de un número complejo en forma binómica z = a + bi, se trata del ángulo que forma el vector
La ecuación anterior tiene infinitas soluciones, ya que debido a los giros, existen infinitos ángulos que la cumplen. Incluso si restringimos α a un ángulo comprendido entre 0 y 2π siempre tendremos dos ángulos que difieren 180º y que poseen la misma tangente. De esta forma para poder concretar exactamente el argumento del número complejo deberemos observar los signos de a y b. Estos signos nos "dirán" en que cuadrante se encuentra el ángulo y por tanto podremos escoger el correcto de los dos posibles.
Determinados argumentos nos pueden dar información concreta del tipo de número complejo que lo posee. En concreto si:
| Argumento | Número Complejo |
|---|---|
| 0º | Número real positivo (a > 0 y b = 0) |
| 90º | Número imaginario puro positivo (a = 0 y b > 0) |
| 180º | Numero real negativo (a < 0 y b = 0) |
| 270º | Número imaginario puro negativo (a = 0 y b < 0) |
Expresión de un número complejo en forma polar a partir de su forma binómica
Un número complejo en forma binómica a+bi cuyo afijo es P se puede expresar en forma polar como mα donde m es el módulo, valor absoluto o longitud del vector
a + bi = mα
Expresión de un número complejo en forma binómica a partir de su forma polar
Si aplicamos las definiciones de seno y coseno sobre el vector
Si sustituimos los valores de a y b sobre la expresión general de la forma binómica a+bi, obtenemos la manera de convertirlo a forma polar.
Un número complejo en forma polar mα se puede expresar en forma binómica a + bi mediante la siguiente expresión:
a + bi = (m · cos α) + (m · sen α) i
Propiedades de los números complejos en forma polar
- Dos números complejos mα = m'β son iguales si los módulos son iguales y además se cumple que sus argumentos difieren un múltiplo entero de 360º.
- El conjugado (
- El opuesto (-Z) de un número complejo Z en forma binómica es un número complejo que comparten la misma parte real e imaginaria aunque cambiadas de signo. Gráficamente, (Z y -Z) se representan simétricos con respecto al origen de coordenadas, por tanto, en forma polar, el opuesto de un número
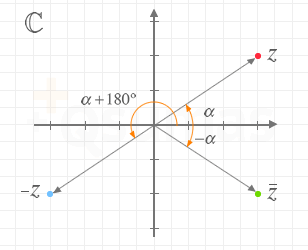
Números complejos conjugados y opuestos en forma polar
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
