Ecuación de la Circunferencia

Se denomina circunferencia al lugar geométrico de los puntos del plano que equidistan de otro punto fijo denominado centro.

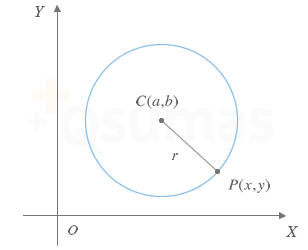
Circunferencia

En la figura se muestra una circunferencia. Observa que cualquier punto P(x,y) de la circunferencia se encuentra siempre situado a la misma distancia de un punto C(a,b) denominado centro. Dicha distancia se denomina radio r de la circunferencia.

Si consideramos que la distancia entre cualquier punto P(x,y) a su centro C(a,b) se denomina radio y vale r, entonces:

$$d\left(P,C\right)=r=\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}$$

Elevando al cuadrado ambos miembros de la ecuación obtenemos que:

$$\begin{gathered} {\left(\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}\right)}^2={\left(r\right)}^2 \Rightarrow \\ {x}^2-2ax+a^2+y^2-2by+b^2=r^2 \Rightarrow \\ {x}^2+y^2+mx+ny+p=0 \end{gathered}$$

Existencia de una circunferencia

Como podrás suponer, no todas las combinaciones de m, n y p de la ecuación $x^2+y^2+mx+ny+p=0$ representan a una circunferencia. En concreto se cumple que:

• Si $a^2+b^2-p>0$, la circunferencia existe.
• Si $a^2+b^2-p=0$, la circunferencia es tan solo un punto ya que su radio es cero.
• Si $a^2+b^2-p<0$, la circunferencia NO existe.

Cálculo del centro y del radio de una circunferencia

Cuando disponemos de la ecuación de una circunferencia en la forma $x^2+y^2+mx+ny+p=0$  podemos determinar su centro por medio de la siguiente expresión:

$$C\left(\frac{-m}{2},\frac{-n}{2}\right)$$

De igual forma se puede obtener su radio utilizando la ecuación:

$$R=\frac{1}{2}\sqrt{m^2+n^2-4p}$$

Casos particulares de circunferencias

Ecuación de una circunferencia centrada en el origen.

Cuando una circunferencia tiene su centro en el origen de coordenadas C(0,0) es posible sustituir las coordenadas de este punto en su ecuación de tal forma que:

$$\begin{gathered} \sqrt{{\left(x-0\right)}^2+{\left(y-0\right)}^2}=r \Rightarrow \\ \boxed{x^2+y^2=r^2} \end{gathered}$$

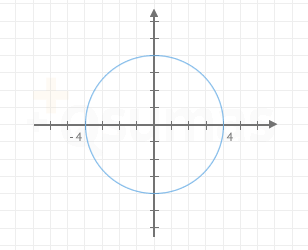
Circunferencia centrada en el origen

En la figura se muestra una circunferencia centrada en el origen. Puedes observar que su radio es 4 por lo que su ecuación es:

$$x^2+y^2=4^2$$

Ecuación de una circunferencia que pasa por el origen.

Cuando una circunferencia de ecuación $x^2+y^2+mx+ny+p=0$ pasa por el origen de coordenadas se cumple que:

$$\begin{gathered} 0^2+0^2+m·0+n·0+p=0 \Rightarrow \\ p=0 \end{gathered}$$

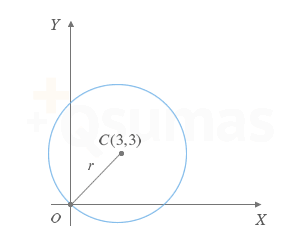
Circunferencia que pasa por el origen

En la figura se muestra una circunferencia centrada en (3,3) que pasa por el origen de coordenadas. Observa que su ecuación, al igual que todas las circunferencias que cortan al origen, no posee coeficiente p:

$$x^2+y^2-6x-6y=0$$

Ecuación de dos circunferencias concéntricas

Si observas bien la ecuación $x^2+y^2+mx+ny+p=0$ el único término que depende directamente del radio es p. Por tanto, dos circunferencias concéntricas (centradas en el mismo punto y con radio distinto) diferirán en este coeficiente.

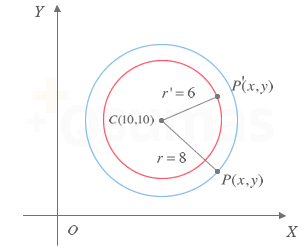
Circunferencias Concéntricas

En la figura se muestran dos circunferencias. Dado que poseen el mismo centro y distinto radio, ambas son concentricas. Comprueba que en sus ecuaciones, al igual que en todas las ecuaciones de circunferencias concéntricas, todos los coeficientes son idénticos excepto el valor de p.

$$\begin{gathered} \mapsto x^2+y^2-20x-20y+164=0 \\ \mapsto x^2+y^2-20x-20y+136=0 \end{gathered}$$