Péndulo cónico

Datos

m = 4200 gr = 4.2 kg
L = 150 cm = 1.5 m
R = 50 cm = 0.5 m
g = 9.8  m/s²

v?
T?

Cuestión a)

Resolución

Si realizamos el diagrama de cuerpo libre de la masa, obtendremos algo similar a lo siguiente:

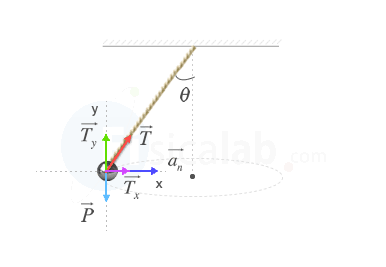
El péndulo cónico se mueve realizando un m.c.u., esto implica que la única aceleración que posee el cuerpo es la aceleración centrípeta. Aplicando el principio fundamental o segunda ley de Newton para la fuerza resultante en cada eje, y teniendo en cuenta que la única aceleración que existe se produce en el eje x (a_x=a_n, a_y = 0):

Eje X

$$\begin{gathered} {\sum }_{}{F}_x=m·a_x \Rightarrow \\ {T}_x = m·a_n \Rightarrow \\ T·\sin \left(\theta \right)=m·\frac{v^2}{R} \left[1\right] \end{gathered}$$

Eje Y

$$\begin{gathered} {\sum }_{}{F}_y=m·a_y \Rightarrow \\ {T}_y-P = m·0 \Rightarrow \\ {T}_y=P \Rightarrow \\ T·\cos \left(\theta \right)=m·g \left[2\right] \end{gathered}$$

Si dividimos miembro a miembro, las ecuaciones [1] y [2], obtenemos la siguiente expresión:

$$\begin{gathered} \frac{\cancel{T}·\sin \left(\theta \right)}{\cancel{T}·\cos \left(\theta \right)}=\frac{\cancel{m}·{\displaystyle \frac{v^2}{R}}}{\cancel{m}·g}\Rightarrow \\ \tan \left(\theta \right)=\frac{v^2}{g·R} \left[3\right] \end{gathered}$$

Si despejamos la v en [3]:

$$v=\sqrt{g·R·\tan \left(\theta \right)} \left[4\right]$$

Conocemos el valor de g y el valor de R, pero desconocemos el angulo θ. Sin embargo, si aplicamos la definición de seno:

$$\begin{gathered} \sin \left(\theta \right)=\frac{R}{L}\Rightarrow \\ \sin \left(\theta \right)=\frac{0.5}{1.5}\Rightarrow \\ \theta ={\sin }^{-1}\left(0.33\right) \Rightarrow \\ \boxed{\theta =19.47º} \end{gathered}$$

Sustituyendo ahora todos los valores en [4]:

$$\begin{gathered} v=\sqrt{g·R·\tan \left(\theta \right)} \Rightarrow \\ v=\sqrt{9.8*0.5*\tan \left(19.47\right)} \Rightarrow \\ \boxed{v=1.31 m/s} \end{gathered}$$

Cuestión b)

Dado que conocemos el valor de θ, m y g, si los sustituimos en la ecuación [2], podremos calcular el valor de la tensión de la cuerda:

$$\begin{gathered} T·\cos \left(\theta \right)=m·g \Rightarrow \\ T=\frac{m·g}{\cos \left(\theta \right)} \Rightarrow \\ T = \frac{4.2·9.8}{\cos \left(19.47\right)} \Rightarrow \\ \boxed{T=43.78 N} \end{gathered}$$