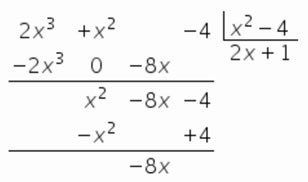Representación función racional
Enunciado
Representa las funciones racionales indicadas a partir de sus expresiones analíticas:
Solución
Consideraciones previas
Para la representación de funciones racionales seguiremos los pasos indicados en el apartado teórico. Por otro lado, ya hemos realizado un ejercicio sobre la monotonía de estas funciones racionales, por lo que nos valdremos de esos resultados cuando sea necesario.
Finalmente, como detalle, observa que las dos primeras funciones son racionales impropias y la tercera es racional propia.
Resolución
1.-
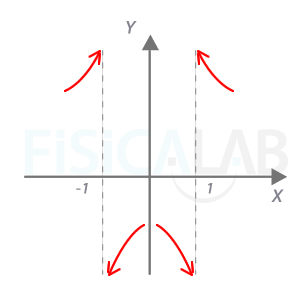
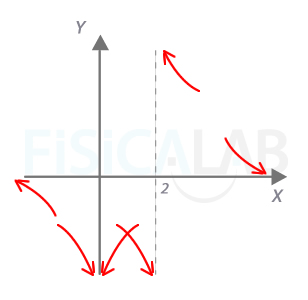
Comenzamos calculando las asíntotas verticales...
Para ver la posición de la curva respecto a ella, utilizamos límites:
En segundo lugar, como el grado del numerador coincide con el grado del denominador, la función tendrá asíntotas horizontales. Vamos a estudiarlas a través de los límites:
Debemos saber si la función se aproxima a la asíntota por encima o por debajo. Para ello damos valores de x muy grandes, y comprobamos si los correspondientes valores de y son un poquito mayores que uno o un poquito menores. En este caso es evidente que son un poquito mayores que uno (al sumar uno en el numerador y restarlo en el denominador, el numerador siempre va a ser mayor). Podemos, así, ir completando el esbozo:
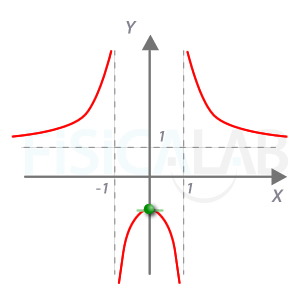
El tercer paso consiste en buscar los puntos singulares tales que f'(x)=0. Ya lo hemos hecho en el ejercicio indicado, obtenido que x=0 f(0)=-1 es un máximo.
Ya estamos en disposición de hacer una representación. Saber que la función presenta simetría par, f(x)=f(-x), nos ayudará con la misma:
2.-
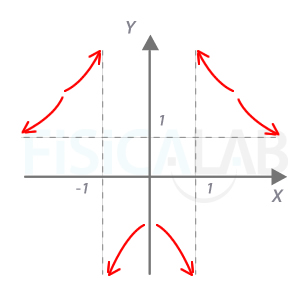
Empezamos buscando las asíntotas verticales. Para ello hacemos 0 el denominador:
Y estudiamos la posición de la curva respecto a tales puntos:
Podemos hacer un primer esbozo:
Ahora, como el grado del polinomio del numerador es exactamente uno superior al del denominador, debemos buscar las asíntotas oblículas. Para ello dividimos el polinomio del numerador entre el del denominador, y el resto es, justamente, la ecuación de la asíntota oblicua buscada:
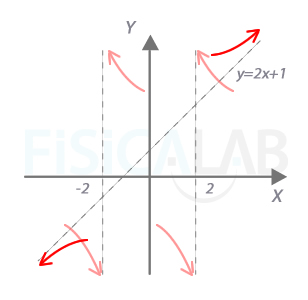
Es decir, la recta y=2x+1 es la asíntota oblicua. Para evaluar la posición de la curva respecto a la asíntota damos valores de x muy grandes y muy pequeños, y sustituimos tanto en la función como en la asíntota para comprobar cuál queda por encima. Así:
- x=20, f(20)=41,4 > y20=41
- x=-20, f(-20)=-39,4< y-20=-39
Completamos nuestro esbozo:
Ahora vamos a por los puntos singulares. Ya han sido resueltos en el ejercicio relacionado, quedando:
- x=-√12, f(-√12)=-9,39 es un máximo
- x=√12, f(√12)=11,39 es un mínimo
- x=0, f(0)=1 es un punto silla
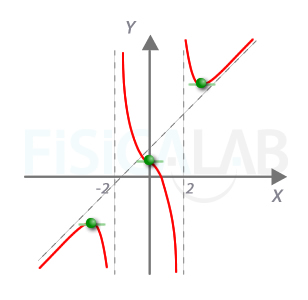
Uniendo los puntos con las ramas podemos hacer nuestra representación final.
3.-
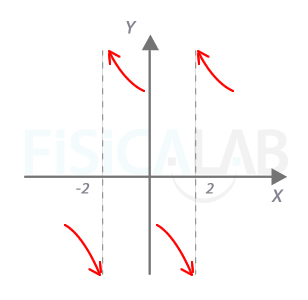
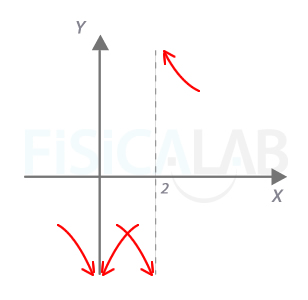
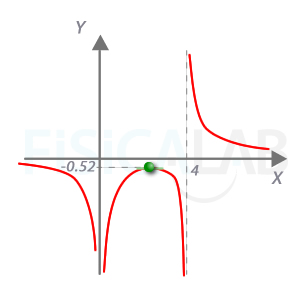
Comenzamos por las asíntotas verticales. Igualando a 0 el denominador tenemos como candidatos x=0 y x=4. Veamos como se el comportamiento de la curva respecto a ellas:
En cuanto a la asíntota horizontal (grado denominador es más de un grado mayor que grado numerador), nos queda:
Por tanto, y=0 es una asíntota horizontal, tanto por la derecha como por la izquierda. Podemos ver el comportamiento de la función en valores muy grandes de x, o muy pequeños, para concluir:
- f(-100)<0
- f(100)>0
Calculamos los puntos singulares. Consulta el ejercicio vinculado para detalles. Debe quedarte:
- x=8/3, f(8/3)=-0,52 es un máximo
Uniendo los puntos, podemos esbozar la gráfica final:
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.