Funciones Racionales

La fuerza que ejerce la gravedad en función de la separación de las masas, la eléctrica en función de la separación de las cargas o la concentración de un fármaco en sangre en función del tiempo transcurrido desde su administración son, todos ellos, ejemplos habituales de funciones racionales. A lo largo de los siguientes puntos vamos a ir desgranando las propiedades de este tipo de funciones:

• Definición
• Gráficas
• Dominio
• Recorrido o imagen
• Continuidad y derivabilidad
• Monotonía y extremos
• Curvatura y puntos de inflexión
• Cortes con los ejes x e y y cambios de signo
• Asíntotas y ramas
• Simetría
• Representación
• Clasificación
• Aplicaciones prácticas

¿Preparado para un viaje racional?

Definición

Como ves, las funciones racionales están estrechamente relacionadas con las polinómicas. Te recomendamos que visites el apartado asociado antes de estudiarlas.

Ejemplos

$$\begin{array}{cc}\mathit{a}\mathbf{)} f\left(x\right)=\frac{3x^2+x+1}{x-1}& \mathit{b}\mathbf{)} f\left(x\right)=\frac{x}{x^3-2}\\ \mathit{c}\mathbf{)} f\left(x\right)=\frac{x+1}{x-1}& \mathit{d}\mathbf{)} f\left(x\right)=\frac{x}{x-1}+1\end{array}$$

Observa que:

• El grado de P(x)>Q(x) en a)
• El grado de P(x)<Q(x) en b)
• Los grados de P(x) y Q(x) son iguales en c)
• La función en d) no está en la forma descrita, pero haciendo unos pequeños ajustes podemos convertirla: $f\left(x\right)=\frac{x}{x-1}+1=\frac{x+x-1}{x-1}=\frac{2x-1}{x-1}$

Por otro lado, atendiendo a las restricciones indicadas podemos decir que no son funciones racionales:

$$\begin{array}{cc}\mathit{a}\mathbf{)} f\left(x\right)=\frac{x+1}{x^2-1}& \mathit{b}\mathbf{)} f\left(x\right)=\frac{x^2+5x-1}{4}\\ \mathit{c}\mathbf{)} f\left(x\right)=\frac{x+\sqrt{x-1}}{x-1}& \mathit{d}\mathbf{)} f\left(x\right)=\frac{1+x}{1+{\displaystyle \frac{1}{x}}}\end{array}$$

¿Sabrías decir por qué? Efectivamente:

• La función en a) no es irreducible, pues tiene raíces comunes con el denominador: $\frac{x+1}{x^2-1}=\frac{x+1}{\left(x+1\right)\left(x-1\right)}=\frac{1}{x-1}$
• La función en b) tiene Q(x) de grado 0 (solo un término independiente), y es, por tanto, de una función polinómica $f\left(x\right)=\frac{x^2+5x-1}{4}=\frac{1}{4}{x}^2+\frac{5}{4}x-\frac{1}{4}$
• La función en c) tiene radicales en el numerador, con lo que P(x) no es un polinomio
• La función en d) tampoco tiene un polinomio en el denominador

Gráficas

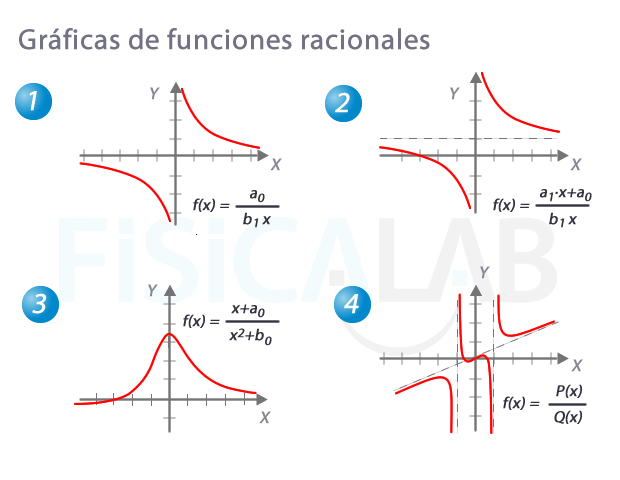
Las gráficas de las funciones racionales se caracterizan por describir curvas suaves, y presentar distintos tipos de asíntotas. Veamos las gráficas más comunes.

Gráficas de funciones racionales

En la imagen puedes ver las gráficas de distintas funciones racionales. En 1 y 2 está la función de proporcionalidad inversa, en dos de sus formas habituales: centrada en el origen (1) y desplazada hacia arriba (2). En 3 y 4 tenemos dos funcionaes racionales arbitrarias. Como veremos al estudiar las asíntotas, en 3 el grado del denominador deber ser mayor, y en 4 el grado del numerador debe ser un grado superior al grado del denominador (de ahí la asíntota oblicua). Por otro lado, observa que las curvas descritas son suaves en todos los casos.

Puedes utilizar este simulador para ver como afectan los distintos parámetros a las gráficas de las funciones racionales.

Un poco más adelante te diremos como puedes esbozar su gráfica a partir de la expresión analítica de la función. Por ahora, vamos a seguir viendo otras características que debes tener presentes.

Dominio

El dominio de definición de la función racional es el conjunto de valores que puede tomar la variable independiente x. Sabemos que en matemáticas no se puede dividir entre 0, de ahí que los valores que anulen el denominador haya que excluirlos del dominio. Nos queda pues $Do{m}_f=\left\{x\in \mathrm{ℝ}/Q\left(x\right)\ne 0\right\}$.

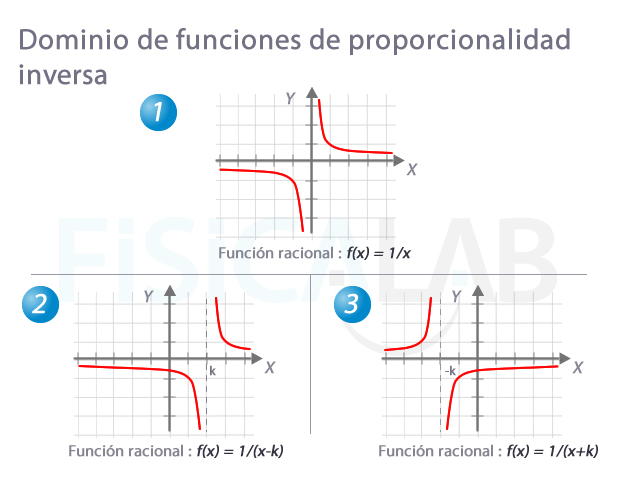
Dominio de funciones racionales

El caso más simple de función racional es el de la función de proporcionalidad inversa 1/x. En ese caso, la gráfica resulta una hipérbola equilátera. Restando o sumando una constante k al denominador desplazamos la gráfica hacia la izquierda o la derecha respectivamente. Observa que, en cada caso, el valor que anula el denominador es el que hay que excluir del dominio, resultando en una asíntota vertical.

Para profundizar en el estudio del dominio de funciones racionales, consulta el punto de funciones racionales en el apartado dedicado al dominio de definición.

Recorrido o imagen

No existe una regla sencilla y general para calcular el dominio de funciones racionales. En general, te recomendamos que esboces la gráfica de la misma, estudiando sus extremos y asíntotas, para así poder deducir el recorrido. No obstante, en algunos casos podremos aplicar el método de la inversa.

Ejemplo

$$f\left(x\right)=\frac{2}{x+1}$$

Su función inversa es:

$$f^{-1}\left(x\right)=\frac{2-x}{x}$$

Siendo Dom(f^-1)=ℝ-{0}, con lo que podemos decir que Rec(f)=ℝ-{0}.

Contiuidad y derivabilidad

Por tanto, antes de dar los intervalos de continuidad y derivabilidad debes estudiar el dominio de la función.

Monotonía: Máximos y mínimos

Para determinar los intervalos de crecimiento y decrecimiento, así como los extremos de una función racional seguiremos el procedimiento habitual. A modo de ejemplo, puedes consultar el siguiente ejercicio del apartado sobre cálculo de extremos.

Curvatura: Concavidad y convexidad

Para determinar los intervalos de concavidad y convexidad, así como los puntos de inflexión de la curva, seguiremos el procedimiento habitual.

Cortes con los ejes

Cortes con eje x

Se trata de hacer f(x)=0 y despejar, lo cual es equivalente a igualar a 0 el polinomio del numerador P(x). Nos quedará una ecuación de grado n, con lo que:

Ya sabes que llamamos ceros a los puntos de corte con el eje x. Son importantes porque en ellos puede cambiar el signo de la función.

Corte con eje y

Para buscar el punto de corte con el eje y en primer lugar debemos cerciorarnos que x=0 pertenece al dominio de nuestra función. Si está, sustituimos y obtenemos el resultado: el valor de la función que nos queda es el cociente de los términios independientes de los polinomios.

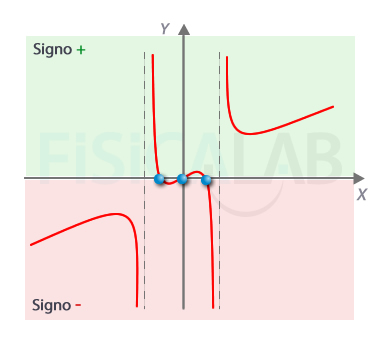
Cortes y signo de una función racional

En la figura está representada una función racional y sus correspondientes ceros. Recuerda que el cambio de signo se puede producir en los ceros, pero también en los puntos que anulan el denominador, esto es, en las asíntotas verticales.

Asíntotas y ramas parabólicas

El estudio de las asíntotas y las ramas parabólicas es muy importante para hacer un bosquejo de una función racional. Se hace mediante límites.

Asíntotas verticales

• Comenzamos haciendo el denominador Q(x)=0. Cada valor de x obtenido será una asíntota vertical

• Una vez hecho esto podemos estudiar los límites laterales para saber la posición de la curva respecto a la asíntota, es decir, si la curva se acerca a ∞ o -∞ por cada lateral. Así, llamando genéricamente x_AV a los valores obtenidos del punto anterior, nos queda:

  $$\underset{x\to {x_{AV}}^{-}}{\lim }f\left(x\right) ;\hspace{0.17em}\underset{x\to {x_{AV}}^{+}}{\lim }f\left(x\right)$$

Asíntota horizontal, oblicua ó ramas parabólicas

Dependerán de la relación entre los grados de P(x) y de Q(x).

• Grado P(x) ≤ grado Q(x) : asíntota horizontal

Hacemos:

$$\underset{x\to \infty }{\lim }f\left(x\right)=\underset{x\to \infty }{\lim }\frac{P\left(x\right)}{Q\left(x\right)}=k$$

Siendo la asíntota horizontal y=k. Ten presente que, en las funciones racionales, de existir asíntota horizontal, es la misma para x→∞ y x→-∞. No obstante, para bosquejar la función es importante estudiar la posición de la curva respecto a ella, esto es, si se acerca a la función "por arriba" o "por abajo". Puedes hacer esto dando a x valores suficientemente grandes o suficientemente pequeños

• Grado P(x) = grado Q(x) + 1 : asíntota oblicua

  Hacemos la división polinómica P(x)/Q(x), y el cociente, en la forma m·x+n es la asíntota oblicua y=m·x+n

  En caso de que la función cuente con asíntotas oblicuas, y si queremos hacer un bosquejo, es importante saber la posición de la curva respecto a la asíntota. Se procede en este sentido de manera similar a las asíntotas horizontales

• Grado P(x) > grado Q(x) + 1 : ramas parabólicas

  En este caso existen ramas parabólicas. Si necesitamos bosquejar la función y saber si la curva se hace ∞ o -∞ por el lateral izquierdo o por el derecho de la gráfica, hacemos:

  $$\underset{x\to \infty }{\lim }f\left(x\right) \hspace{0.17em}; \underset{x\to -\infty }{\lim }f\left(x\right)$$

Simetría

Las funciones racionales pueden ser simétricas.

• Pueden presentar simetría impar, respecto al origen

  $$-f\left(x\right)=f\left(-x\right)$$

• O simetría par, respecto al eje y

  $$f\left(x\right)=f\left(-x\right)$$

Representación

Te recomendamos que sigas los siguientes pasos para la representación gráfica de funciones racionales:

1. Busca las asíntotas verticales, y estudia la posición de la curva respecto a las mismas
2. Busca las asíntotas horizontales u oblicuas y estudia la posición de la curva respecto a las mismas
3. Si no hay asíntotas horizontales u oblicuas, estudia las ramas parabólicas
4. Buscamos los puntos singulares, esto es, aquellos en los que f'(x)=0. Encuentra el punto completo (coordenada x y coordenada y). En los puntos singulares la función racional presenta una tangente horizontal (pueden ser máximos, mínimos o puntos silla)

5. Si deseamos una representación un poco más precisa, se buscan los puntos de corte con los ejes, tal y como hemos señalado más arriba.

   También podemos seleccionar valores de x cualesquiera y obtener su imagen para perfiilar la función con mayor precisión.

6. Finalmente se unen los puntos obtenidos con las asíntotas, teniendo especial cuidado de dibujar solo los puntos singulares obtenidos.

Una vez representada, puedes ayudarte de este simulador para verificar que la gráfica es correcta.

Tipos

Podemos distinguir dos grandes grupos de funciones racionales:

• Funciones racionales propias

  Son aquellas en las que el grado del denominador es mayor.

• Funciones racionales impropias

  Son aquellas en las que el grado del numerador es mayor o igual que el del denominador. Su principal característica es que se pueden dividir en una suma de función racional propia más un polinomio. Observa el siguiente ejemplo:

  $$f\left(x\right)=\frac{x^2-4}{x-1}=x+1+\frac{-3}{x-1}$$

  Recuerda que, para hacer la conversión aplicamos la regla de la división en la división de polinomios: Cociente·Divisor+Resto=Dividendo⇒ Dividendo/Divisor=Cociente+Resto/Divisor

  En estos casos, el comportamiento de la función para valores suficientemente grandes (en valor absoluto) de x está gobernado por el polinomio, lo cual nos puede simplificar enormemente su análisis.

Aplicaciones

Dada su variaedad, es habitual utilizar las funciones racionales para aproximar otras más complejas, no obstante hay muchos fenómenos reales que pueden ser descritos mediante este tipo de funciones. Por ejemplo:

• La corriente que pasa por un cable en función de la resistencia del mismo
• El potencial gravitatorio en función de la distancia
• El tiempo que puede un profesor dedicar a cada alumno individualmente, en función del número de alumnos que acuden a la hora de tutoría