Funciones Exponenciales

El crecimiento de contagios en una pandemia como la COVID-19 ó la evolución de una población de insectos en un determinado lugar son fenómenos que pueden describirse mediante una función exponencial. A lo largo de los siguientes epígrafes vamos a ir desgranando las propiedades de este tipo de funciones:

• Definición
• Gráficas
• Dominio
• Recorrido o imagen
• Continuidad y derivabilidad
• Monotonía, máximos y mínimos
• Curvatura
• Cortes con los ejes x e y y cambios de signo
• Asíntotas y ramas
• Simetría
• Representación
• Aplicaciones prácticas

Para ayudarte a estudiar todas estas propiedades te aconsejamos que te ayudes de este simulador de funciones exponenciales que hemos preparado. Queremos que tu conocimiento también aumente de manera exponencial. ¿Estás preparado?

Definición

Ejemplos

$$\begin{array}{cc}\mathit{a}\mathbf{)} f\left(x\right)=3^x& \mathit{b}\mathbf{)} f\left(x\right)=5·2^x\\ \mathit{c}\mathbf{)}\mathbf{ } f\left(x\right)=-5·e^{x+3}& \mathit{d}\mathbf{)} f\left(x\right)={\left(\sqrt{3}\right)}^x\\ \mathit{e}\mathbf{)} f\left(x\right)={\left(1/2\right)}^x& \mathit{f}\mathbf{)} f\left(x\right)=0.7^{x-7}\\ \mathit{g}\mathbf{)} f\left(x\right)=e^{2x}\hspace{0.17em}& \mathit{h}\mathbf{)}\hspace{0.17em}f\left(x\right)=3^{-x}\end{array}$$

Observa que:

• Las funciones en a), d) y e) son funciones exponenciales sencillas, en la forma expresada en la definición. El resto presentan algunas variaciones, pero siguen siendo funciones exponenciales. Veámos el porqué...

• La función en b) presenta un coeficiente que multiplica a la base. Cuando multiplicas un número por una función exponencial de la forma a^x, estas quedan escaladas en el eje y y por tanto crecen (o decrecen) más rápidamente

• La función en f) presenta una resta en el exponente. Siempre que se suma o resta un número real a la variable independiente puedes entender que se produce un desplazamiento horizontal de la función exponencial original a^x. Otra forma de verlo es a partir de las propiedades de las potencias

  $$f\left(x\right)=0.7^{x-7}\underset{a^{b+c}=a^b·a^c}{=}0.7^x·0.7^{-7}\underset{a^{-b}=\frac{1}{a^b}}{=}\frac{1}{0.7^7}·0.7^x$$

• La función en c) combina ambas transformaciones

• La base es, en todos los casos, un real positivo distinto de 1. Ten presente que, en el caso c) el signo menos es del coeficiente que multiplica a la función. Puedes pensar en él como una reflexión vertical de la función original

• La función en h) presenta un signo - acompañando a la variable independiente. Puedes pensar en él como una reflexión horizontal de la función original, o bien:

  $$f\left(x\right)=3^{-x}=\frac{1}{3^x}={\left(\frac{1}{3}\right)}^x$$

• Finalmente, la función en g) presenta un coeficiente multiplicando a la variable independiente. Puedes pensar en él como una escalado horizontal de la función, o bien aplicar las propiedades de las potencias:

  $$f\left(x\right)=e^{2x}\underset{a^{bc}={\left(a^b\right)}^c}{={\left(e^2\right)}^x}$$

A lo largo del resto de epígrafes nos centraremos principalemente en la función exponencial más sencilla f(x)=a^x. A partir de ella podrás estudiar las infinitas variaciones que se pueden dar.

Gráficas

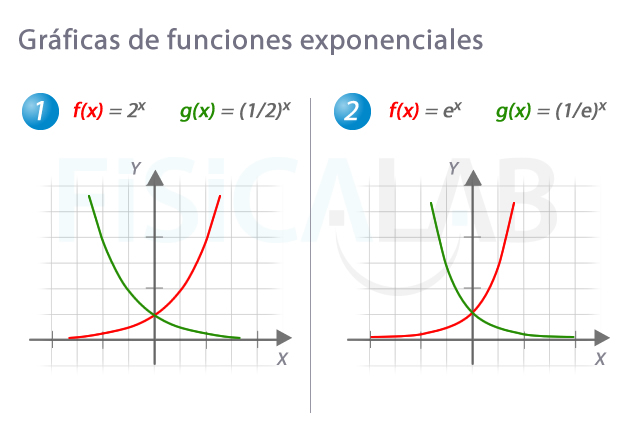
Funciones exponenciales

Las gráficas en rojo corresponden a dos exponenciales de base mayor que 1. Observa como un pequeño cambio en la base provoca un cambio en el crecimiento muy pronunciado (la función f(x)=e^x, por ejemplo, crece mucho más rápidamente que f(x)=2^x). Por otro lado, las funciones en verde corresponden a dos exponenciales de base menor que 1.

Observa también que cada función en rojo es la simétrica de la correspondiente verde. Esto es así porque g(x)=f(-x):

• g(x)=(1/2)^x=2^-x=f(-x)
• g(x)=(1/e)^x=e^-x=f(-x)

Finalmente, dado que cualquier número distinto de 0 elevado a 0 es 1, las cuatro funciones pasan por (0,1)

Como vimos, también podemos encontrar funciones exponenciales un poco más complejas.

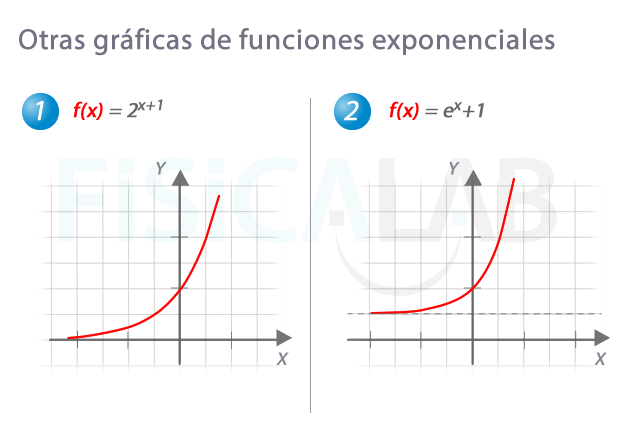
Funciones exponenciales más complejas

La gráfica en 1 se puede obtener a partir de la de 2^x, desplazándola una unidad a la izquierda. Observa que 2^x+1=2·2^x. En este caso, las funciones de tipo b·a^x pasan por el punto (0,k). Por otro lado, la función en 2 la hemos obtenido desplazando una unidad hacia arriba la función original.

Como ves, en todos estos casos, las exponenciales son inyectivas, pues no existen dos valores de y iguales para la misma x.

Dominio

En el caso de funciones más complejas de tipo f(x)=a^g(x) el dominio de la exponencial coincidirá con el dominio de g(x).

Ejemplo

El dominio de la función f(x)=e^1/x es $Do{m}_f=\mathrm{ℝ}-\left\{0\right\}$.

Si deseas ampliar información sobre cómo calcular el dominio de una función cualquiera, consulta el apartado vinculado.

Imagen o recorrido

Veamos el recorrido de algunas funciones exponenciales tipo.

Continuidad y derivabilidad

Esto se cumple para la mayoría de funciones exponenciales sencillas:

• $5^x$
• ${\left(\frac{1}{3}\right)}^{x-3}$
• $-3^{x+2}$

Sin embargo, nos podemos encontrar exponenciales más complejas, fruto de la composición de funciones, cuyo estudio requiere más elaboración. Así, por ejemplo, la función $f\left(x\right)=e^{\sqrt[3]{x}}$ tiene su variable independiente afectada de una raíz. En este caso la función es continua en el conjunto de los reales, pero no es derivable en x=0.

Nota: Visita, si lo necesitas, el apartado sobre funciones con raíces para aclarar por qué sucede esto.

Monotonía y extremos

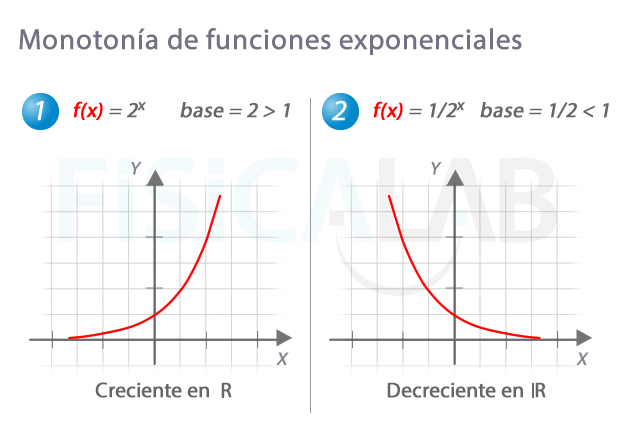
Crecimiento y decrecimiento en exponenciales

Como ves, si la base es mayor que 1, caso de la imagen izquierda, a medida que tomamos valores mayores de la abscisa x los valores de la ordenada y se van haciendo más grandes también. Por eso es creciente. En caso de que la base esté en el intervalo (0,1) (imagen derecha) a medida que tomamos valores mayores de la abscisa x los valores de en el eje y se van haciendo más pequeños. Por eso es decreciente.

Para funciones exponenciales más complejas te recomendamos que sigas los pasos habituales para el estudio de la monotonía.

Curvatura y puntos de inflexión

Para funciones exponenciales más complejas te recomendamos que sigas los pasos habituales para el estudio de la cuirvatura.

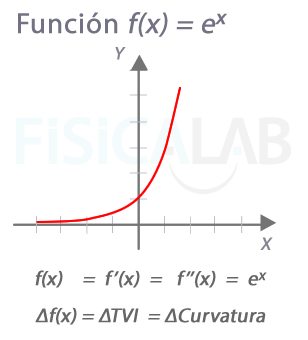
Particularidad de e^x

Observa que en la función exponencial f(x)=e^x coinciden la derivada primera, la segunda, y todas las sucesivas, tal y como estudiamos en las reglas de derivación. ¿Qué implicación tiene esto?

Efectivamente, tomados dos valores cualesquiera de x, la separación entre ellos coincide con la variación de su tasa de variación instantánea (crecimiento) y con la variación de la curvatura.

Cortes con los ejes

Corte con eje x

El procedimiento habitual consiste en hacer f(x)=0 y despejar la variable independiente x. En el caso de las funciones tipo a^x,a^x=0 no tiene solución. ¿Sabrías decir por qué?

Efectivamente, las funciones del tipo a^x no presentan ningún corte con el eje x, y por tanto ningún cambio de signo, ya que cualquier número positivo elevado a otro será siempre positivo.

No obstante, si la función se encuentra desplazada en el eje vertical, sí que puede darse un corte con el eje x.

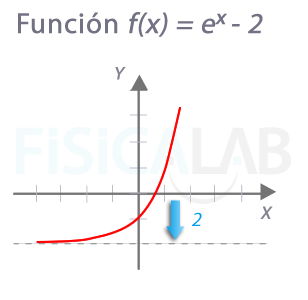
Corte con eje x

El corte con el eje x puede producirse en las funciones exponenciales cuando se encuentran desplazadas. Para determinar el punto exacto resolvemos:

$$e^x-2=0\Rightarrow e^x=2$$

Aplicando logaritmos a ambos lados, y sus propiedades nos queda:

$$\ln \left(e^x\right)=\ln \left(2\right)\underset{\ln \left(a^b\right)=b\ln \left(a\right)}{\Rightarrow }x\ln \left(e\right)=\ln \left(2\right)\Rightarrow x=\ln \left(2\right)$$

Por tanto el punto de corte es (Ln(2),0)

Corte con eje y

En este caso el procedimiento general consiste en hacer x=0 y resolver. Así, en funciones de tipo f(x)=a^x el punto de corte está en (0,1).

No obstante, si hay un desplazamiento horizontal, el corte puede darse en cualquier otro punto del eje y.

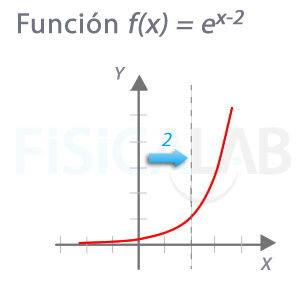
Corte con eje y

El corte con el eje y se produce, en general en el punto (0,1), porque cualquier número elevado a 0 es 1. No obstante, si la función es más compleja, como la de la figura, se puede producir en otro lugar. Para determinar el punto exacto resolvemos:

$$y=e^{0-2}\Rightarrow y=e^{-2}=\frac{1}{e^2}=0.13$$

Por tanto el punto de corte es (0, 0.13).

Asíntotas y ramas

Las funciones exponenciales sencillas tienen 2 tipos de ramas infinitas: 1 rama parabólica y una asíntota horizontal.

• Rama parabólica: Se da cuando:

  $$\underset{x\to \infty }{\lim }f\left(x\right)=\pm \infty \text{ó} \underset{x\to -\infty }{\lim }f\left(x\right)=\pm \infty$$

• Asíntota horizontal: Se da cuando:

  $$\underset{x\to \infty }{\lim }f\left(x\right)=k \text{ó} \underset{x\to -\infty }{\lim }f\left(x\right)=k$$

  Siendo en este caso y=k la asíntota horizontal

Por tanto, en general basta calcular $\underset{x\to \infty }{\lim }f\left(x\right)$ y $\underset{x\to -\infty }{\lim }f\left(x\right)$ para saber dónde está cada una.

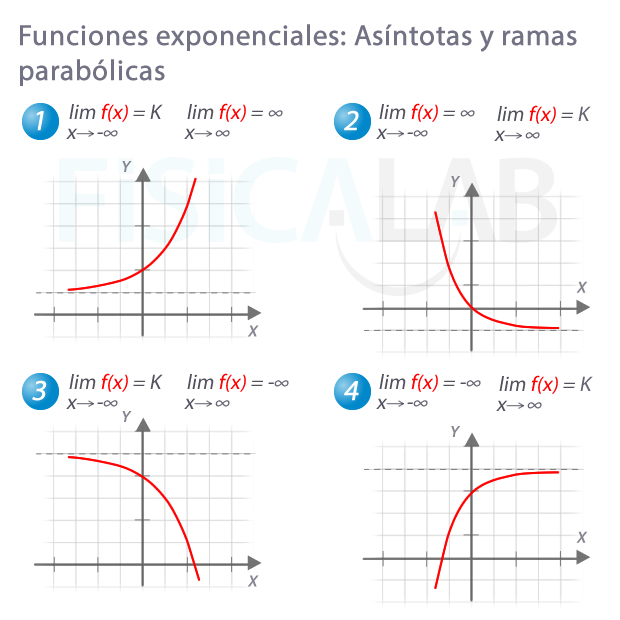
Ramas infinitas en exponenciales

En la imagen superior puedes encontrar las 4 variantes de asíntotas horizontales y ramas parabólcas en exponenciales del tipo a^x. Así, tenemos:

• Asíntota horizontal positiva en 1 y 3
• Asíntota horizontal negativa en 2 y 4
• Rama parabólica positiva en 1 y 2
• Rama parabólica negativa en 3 y 4

Si deseas estudiar el cálculo de ramas infinitas en exponenciales más complejas, visita los apartados enlazados.

Simetría

Las funciones exponenciales sencillas no presentan simetría par ni impar. Lo que sí podemos es encontrar simetría entre las funciones f(x)=a^x y f(x)=(1/a)^x, como se ponía de manifiesto en las imágenes del comienzo de este apartado. También podemos encontrar, tal y como dijimos, una simetría entre la función exponencial f(x)=a^x y la función logarítmica f(x)=log_a(x) respecto a la recta y=x.

Representación

La representación de una función exponencial sencilla es bastante inmediata. Seguiremos los siguientes pasos:

1. Calculamos $\underset{x\to -\infty }{\lim }f\left(x\right)$ y $\underset{x\to \infty }{\lim }f\left(x\right)$ para determinar la posición de la rama parabólica y de la asíntota horizontal
2. Calculamos el punto de corte con el eje y y, si procede, también con el eje x
3. Si deseamos una representación un poco más precisa hacemos una tabla de valores con aquellas x que se encuentren en el entorno en el que queremos precisión
4. Finalmente unimos los puntos obtenidos teniendo en cuenta la forma de una exponencial tipo

Si la función a representar es compleja, como por ejemplo $f\left(x\right)=e^{\frac{1}{x^2}}$, te recomendamos que sigas los pasos genéricos para representación gráfica de funciones.

Aplicaciones

Algunos fenómenos que son descritos mediante exponenciales:

• Crecimiento de poblaciones. El número de individuos N(t) en una población a lo largo del tiempo t viene determinado por la expresión N(t)=N₀·e^k·t siendo N₀ el número de individuos inicial y k una constante denominada tasa de crecimiento (las moscas, por ejemplo, se reproducen más rápido que los humanos, y por ello tendrán un k mayor).

• En economía, la expresión del capital disponible C después de cierto tiempo t de haber depositado un capital inicial C₀ a un interés continuo i viene dada por C=C₀e^i·t

• La ley de enfriamiento de Newton, que establece la evolución de la temperatura T de un cuerpo que se encuentra a una determinada temperatura inicial T_c, cuando se sitúa en un entorno a temperatura T_amb, esto es, T=T_amb+(T_c-T_amb)·e^-k·t.

  

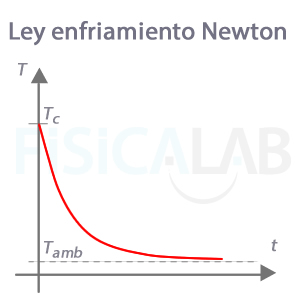
  Ley de enfriamiento de Newton

  En este caso, como puede observarse, la exponencial es decreciente.

• La desintegración de un elemento radiactivo. Así, el número de átomos radiactivos N(t) que quedan a lo largo del tiempo t en una muestra que contaba inicialmente con N₀ átomos radiactivos viene dada por N(t)=N₀·e^-V·t, siendo 1/V una constante denominada constante de semidesintegración

• Algunos fenómenos estadísticos. Así, es habitual encontrar la función de probabilidad $f\left(x\right)=e^{-k{x}^2}$

  

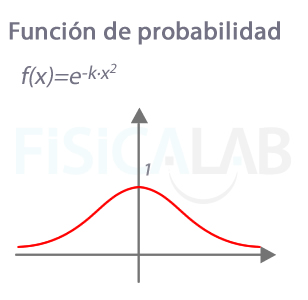
  Función de probabilidad exponencial

  En este caso, como puede observarse, la exponencial es más compleja, al encontrarse elevada a un polinomio de grado 2. De hecho, se trata de una función que presenta simetría par, al contrario de lo que ocurre cuando se encuentran elevadas a un polinomio de grado 1.