Rectas Perpendiculares. Perpendicularidad

Como determinar si dos rectas son perpendiculares

Dos rectas, r y s, se dice que son perpendiculares ( $r ⊥ s$ ) si sus vectores directores ${\vec{v}}_{r}$ y ${\vec{v}}_{s}$ son perpendiculares ( ${\vec{v}}_{r} \cdot {\vec{v}}_{s} = 0$ ) o sus pendientes $m_{r}$ y $m_{s}$ son inversas y cambiadas de signo ( $m_{r} = - \frac{1}{m_{s}}$ ).

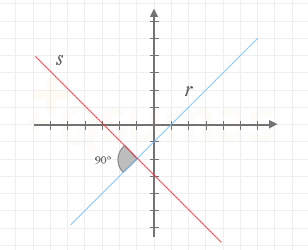
Dos semirrectas con origen común crean dos ángulos.

Rectas perpendiculares

En la figura se muestran dos rectas r y s:

$r \equiv x - y - 1 = 0 s \equiv (x, y) = (1, 4) + λ \cdot (2, - 2)$

Ambas son perpendiculares ya que se cumple que:

$\begin{array}{r} m_{s} = \frac{v_{2}}{v_{1}} = \frac{- 2}{2} = - 1 \\ m_{r} = - \frac{A}{B} = - \frac{1}{- 1} = 1 \end{array}\} m_{r} = - \frac{1}{m_{s}} \Rightarrow 1 = 1$

Recuerda que cuando las rectas se encuentran expresadas en forma general ( $A x + B y + C = 0$ ) la pendiente se puede obtener fácilmente mediante el cociente de las variables A y B de la ecuación general. Así mismo, cuando se encuentra en forma vectorial, paramétrica o continua puede ser útil obtenerla mediante el cociente de las componentes del vector director.

$m = - \frac{A}{B} o m = \frac{v_{2}}{v_{1}}$

Dos rectas r y s son perpendiculares si se cumple:

$m_{r} = - \frac{1}{m_{s}} o {\vec{v}}_{r} \cdot {\vec{v}}_{s} = 0$

donde:

$m_{r}$ y $m_{s}$ son las pendientes de r y s respectivamente.
${\vec{v}}_{r}$ y ${\vec{v}}_{s}$ son vectores directores de r y s respectivamente.

Ejemplo

Determina si las ecuaciones de las rectas r ≡ 4x + 2y + 3 = 0 y s ≡ 4x - 8y + 5 = 0 son perpendiculares.

Ver solución

Cálculo de una recta perpendicular a otra dada

Como hemos visto anteriormente, cuando disponemos de dos rectas expresadas en su ecuación general:

$r \equiv A x + B y + C = 0 s \equiv A' x + B' y + C' = 0$

podemos determinar facilmente si ambas son perpendiculares comprobando que se cumple la siguiente ecuación:

$m_{r} = - \frac{1}{m_{s}} \Rightarrow - \frac{A}{B} = - \frac{1}{- \frac{A'}{B'}} \Rightarrow \frac{- A}{B} = \frac{B'}{A'}$

Observa que el hecho de que dos rectas sean perpendiculares depende de los coeficientes A, B, A' y B' de la ecuación general de sus rectas, nunca de C ni C'. Esto nos permite determinar que siempre que A=-B' y B=A' ambas rectas serán perpendiculares independientemente del valor de C y C'.

Si las ecuaciones generales de dos rectas r y s tienen la siguiente forma, ambas son perpendiculares:

$r \equiv A x + B y + C = 0 s \equiv - B x + A y + K = 0, K \in ℝ$

Ejemplo

Dada la ecuación de la recta 7x - 4y + 1 = 0, determina otra recta distinta que sea perpendicular a ella.

Ver solución

Rectas perpendiculares al eje OX

Cualquier recta r que sea perpendicular al eje OX tiene la forma:

$x = a, a \in ℝ$

Rectas perpendiculares al eje OY

Cualquier recta r que sea perpendicular al eje OY tiene la forma:

$y = a, a \in ℝ$

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.