Potencial gravitatorio de un sistema de cuatro partículas

Enunciado

dificultad

En cada uno de los vértices de un cuadrado de dos metro de lado se distribuyen cuatro masas de 1000 kg que podemos considerar esféricas. Determina la energía potencial gravitatoria que adquirirá una masa considerada puntual de 3 kg situada en el centro del cuadrado suponiendo que los radios de las esferas son de 0.5 m. Posteriormente determina la energía potencial que adquiriría otra masa, también puntual, de 6 kg.

Solución

Datos

Lados del cuadrado: l = 2 m
Valor de las masas: m₁= m₂= m₃= m₄ = 1000 kg
Radio de las masas esféricas: 0.5 m
Masas puntuales situadas en el centro del cuadrado: m_a = 3 kg ; m_b = 6 kg

Consideraciones previas

Para determinar la energía potencial gravitatoria de m_a y m_b , situadas en el centro del cuadrado vamos a calcular previamente el potencial gravitatorio V en dicho punto, que no es más que la energía potencial gravitatoria por unidad de masa en el citado punto. A partir de él, podemos calcular la energía potencial de cualquier masa m a través de la expresión:

$E_{p} = V \cdot m$
Se nos proporciona información de la forma geométrica de las masas que generan el campo. Sabemos que el potencial creado por una masa esférica en el exterior de la misma coincide con el que crearía una partícula puntual situada en el centro de la misma. Dado que los radios de las esferas son de 0.5 m, se puede comprobar fácilmente que el centro del cuadrado queda en el exterior de todas las masas, con lo que podemos aplicar:

$V_{i} = - G \cdot \frac{m_{i}}{r_{i}}$

Si el centro del cuadrado quedase en el interior de alguna de las esferas no podríamos aplicar esta expresión para el cálculo del potencial asociado

Resolución

El potencial total en el centro del cuadrado será la suma de los potenciales que generan cada una de las masas:

$V = V_{1} + V_{2} + V_{3} + V_{4}$

La distancia r al centro del cuadrado es la misma en todos los casos y se puede calcular según el teorema de Pitágoras:

$r^{2} = 1^{2} + 1^{2} \Rightarrow r = \sqrt{2} m$

cuatro masas sobre los vértices de un cuadrado de lado 2 metros

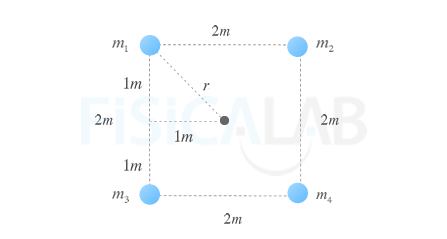
Teniendo en cuenta que también las masas de las partículas son iguales, podemos escribir:

$V = V_{1} + V_{2} + V_{3} + V_{4} = - G \cdot \frac{m_{1}}{r_{1}} - G \cdot \frac{m_{2}}{r_{2}} - G \cdot \frac{m_{3}}{r_{3}} - G \cdot \frac{m_{4}}{r_{4}} = - 4 \cdot G \cdot \frac{m_{1}}{r_{1}} = = - 4 \cdot 6.67 \cdot 10^{- 11} \cdot \frac{1000}{\sqrt{2}} = - 18.8 \cdot 10^{- 8} J / k g$

A partir del potencial es inmediato calcular la energía potencial gravitatoria que adquieren las masas pedidas. Para la masa de 3 kg:

$E_{p} = V \cdot m = - 18.8 \cdot 10^{- 8} \cdot 3 = - 5.65 \cdot 10^{- 7} J$

Para el caso de la masa de 6 kg:

$E_{p} = V \cdot m = - 18.8 \cdot 10^{- 8} \cdot 6 = - 11.28 \cdot 10^{- 7} J$

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Fórmulas

Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.

Fórmulas

Apartados relacionados