Límites a partir de gráficas
Enunciado
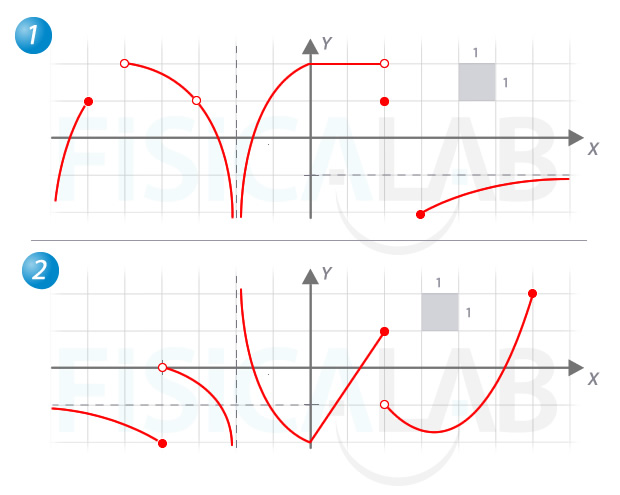
Determina los límites indicados, a partir de las gráficas de las funciones correspondientes. Cuando sea relevante, indica también el valor de los límites laterales:
| Función 1 | Función 2 |
|
|
|
Solución
Consideraciones previas
Recuerda que
Por otro lado, observa en la leyenda de ambas gráficas que cada cuadro de la cuadrícula mide una unidad horizontal por una dimensión vertical.
Resolución
Función 1
En primer lugar, vemos que la función se va a menos infinito en la parte izquierda de la gráfica, por tanto:
Siguiendo con lo que ocurre cuando nos aproximamos a -5, vemos que no hay función más que por la derecha, con lo que:
Continuado, vemos que no existe f(-3), aunque sí está definido su entorno, y con igual valor, tanto por la izquierda como por la derecha. Por tanto:
En x=-2 la función no está definida, pero si en su entorno, apareciendo una asíntota vertical al irse la función a menos infinito en ambos laterales, así pues:
Cuando nos aproximamos a x=0, la función es continua, y no presenta ninguna particularidad adicional, los límites laterales son iguales, y por tanto:
En el caso de x=2, el comportamiento por la izquierda, por la derecha, y en el propio punto es diferente. Observa:
Para el siguiente caso que nos ocupa, x=3, el límite solo existe por la derecha:
Por último, cuando x crece indefinidamente, la función se aproxima a -1 (se trata de una asíntota horizontal). Es decir:
Función 2
En este caso, la función presenta una asíntota horizontal según el primer límite pedido, ya que a medida que la x se hace más negativa, la función se aproxima a un valor concreto: y=-1
Cuando nos aproximamos a -4, hay un comportamiento diferente por la izquierda que por la derecha, por lo que no existe el límite pedido:
Cuando nos aproximamos a -2, la función también tiene un comportamiento diferente por la izquierda y por la derecha. Por tanto, estrictamente hablando, tampoco existe el límite pedido:
Sin embargo, la función se aleja indefinidamente del eje y=0 a medida que se aproxima a la asíntota vertical (decimos "la función diverge"), independientemente de que lo haga hacia más infinito o hacia menos infinito. Por eso es habitual decir que:
Los siguientes dos límites no presentan ninguna particularidad que no hayamos contemplado ya. Así:
Finalmente, no existe el límite cuando x tiende a infinito. La razón es que esta termina con un punto rojo en f(6)=2, indicando así que es el último punto en que se encuentra definida.
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
