Potencia motriz subiendo rampa

Enunciado

dificultad

Un automóvil se mueve horizontalmente con una velocidad constante de 110 km·h^-1. Sabiendo que tiene una masa de 1.4 toneladas (incluyendo ocupantes), determina la potencia motriz extra que debe desarrollar el motor cuando comienza a subir una rampa del 5%.

Solución

Datos

Velocidad: v = 110 km/h = 30.55 m/s
Masa: m = 1.4 t = 1400 kg
Pendiente rampa: 5% => $α = \tan^{- 1} (\frac{5}{100}) = 0.0499 rad$

Resolución

En un principio, cuando el automóvil avanza horizontalmente a velocidad constante, la fuerza motriz del motor se emplea en vencer las fuerzas de fricción (rozamiento con el aire y con el suelo). De este modo, la fuerza resultante se hace 0 y el cuerpo avanza a velocidad constante ( F = m·a ). Cuando el automovil comienza a subir, la fuerza motriz debe incrementarse para contrarestar la componente x del peso, tal y como se observa en la figura.

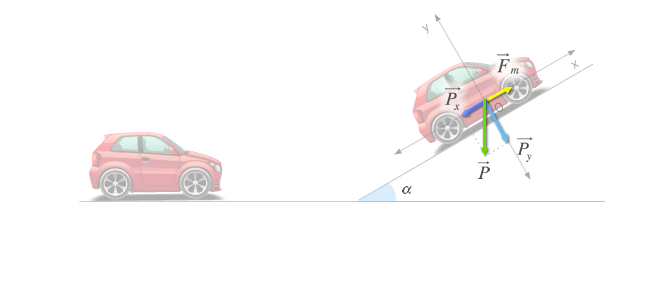
Calcularemos la potencia desarrollada por dicha fuerza extra que llamamos F_m.

$P = \frac{W}{t} = \frac{{\vec{F}}_{m} \cdot ∆ \vec{r}}{t} = \frac{F_{m} \cdot ∆ s}{t} = F_{m} \cdot v;$

El módulo de la fuerza extra es igual al de la componente x del peso:

$F_{m} = P_{x} = m \cdot g \cdot \sin (α) = 1400 \cdot 9.81 \cdot \sin (0.0499) = 695.04 N$

$P = F_{m} \cdot v = 685.04 \cdot 30.55 = 20928.03 W;$

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Fórmulas

Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.

Fórmulas

Apartados relacionados