Fuerza de rozamiento a partir de potencia motriz

Datos

• Velocidad: v = 95 km/h = 26.38 m/s
• Masa: m = 92 kg
• Pendiente rampa: 5% => $\alpha ={\tan }^{-1}\left(\frac{5}{100}\right)=0.0499\text{rad}$

Resolución

Sabemos que la velocidad del ciclista es constante (aceleración nula). Esto quiere decir que, por la Segunda Ley de Newton o Principio Fundamental de la Dinámica, la fuerza resultante sobre el ciclista es también nula. En la siguiente figura aparece un diagrama de fuerzas con la situación.

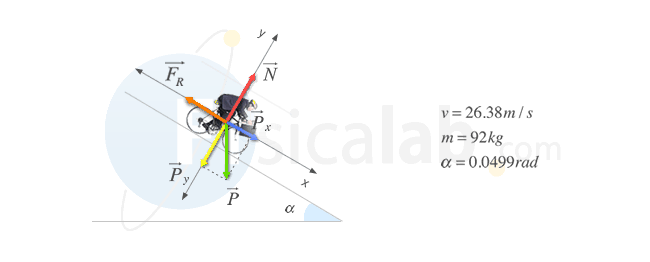
Como puede observarse, la componente x del peso P_x favorece el movimiento y la fuerza de rozamiento F_r se opone a él. Hay que indicar que, en este caso con F_r nos referimos al conjunto de fuerzas de fricción o rozamiento debidas tanto a la fricción con el aire como con el suelo como con cualquier otro elemento que pueda oponerse al movimiento. Vamos a calcular dicha fuerza, sabiendo que la fuerza resultante es cero, tal y como habíamos indicado.

$$F_T=m·\cancel{a}=0; P_x-F_r=0;$$

$$P_x=F_r\Rightarrow m·g·\sin \left(\alpha \right)=F_r;$$

$$F_r=92·9.8·\sin \left(0.0499\right)=\boxed{44.97 \text{N}}$$

O si lo preferimos en notación vectorial y teniendo en cuenta la situación del sistema de referencia representado en la figura:

$$\boxed{{\overrightarrow{F}}_r=-44.97\overrightarrow{i} \text{N}}$$

Por último, para el cálculo de la potencia desarrollado por la componente x del peso P_x:

$$P=\frac{W}{t}=\frac{{\overrightarrow{P}}_x·∆\overrightarrow{r}}{t}=\frac{P_x·∆s}{t}=P_x·v;$$

$$P=92·9.8·\sin \left(0.0499\right)·26.38=\boxed{1186.33 \text{W}}$$