Trabajo realizado por fuerza rozamiento y por peso

Datos

μ = 0.15; 

m = 200 Kg

1.- Partimos de la situación de la figura, en la que hemos hecho una representación de las fuerzas que intervienen en el problema y hemos supuesto un sentido para el movimiento

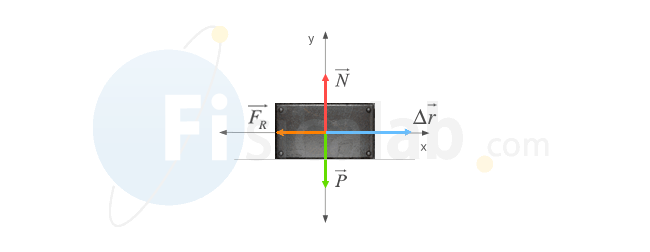
La fuerza de rozamiento se opone al desplazamiento, por lo que podemos decir que forma un ángulo de 180º ó π rad con este. Su módulo viene determinado por:

$$F_r=\mu ·N\underset{\overline{)1}}{\underbrace{=}}\mu ·m·g=0.15·200·9.81=294.3 \text{N}$$ 

Donde hemos aplicado

$$\overline{)1} N=P=m·g$$

Además, g = 9.81 m/s². Con lo anterior nos queda

$$W=\overrightarrow{F_r}·∆\overrightarrow{r}=F_r·∆r·\cos \left(\alpha \right)=294.3·2·\cos \left(\pi \right)=\boxed{-588.66 \text{J}}$$ 

Como puedes ver, el signo del trabajo es negativo, oponiéndose al movimiento y por ello también es llamado trabajo resistente.

Por otro lado, la fuerza peso forma un ángulo de 90º o π/2 rad con el desplazamiento y por tanto, el trabajo desarrollado por esta será nulo (cos(π/2) = 0).

$$W=\overrightarrow{P}·∆\overrightarrow{r}=P·∆r·\cos \left(\alpha \right)=P·∆r·\cancel{\cos \left(\pi /2\right)}=\boxed{0 \text{J}}$$ 

2.- Comenzamos, una vez más, por realizar un diagrama de fuerzas para visualizar adecuadamente la situación.

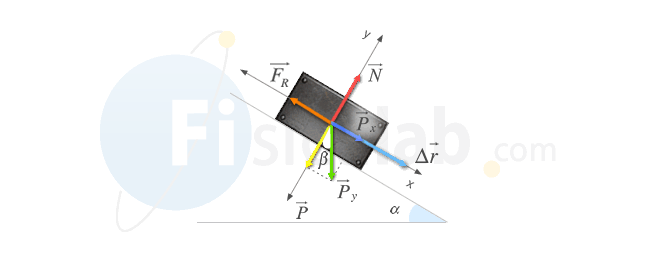
El enunciado del problema nos dice que se produce un desplazamiento de dos metros. En este caso, ese desplazamiento se produce a lo largo del plano inclinado y supondremos que hacia la derecha, tal y como se representó en la figura. Por otro lado, en esta ocasión para el cálculo de la normal hemos de tener en cuenta el ángulo de inclinación del plano, de 25º o 0.436 rad.

$$N=P_y=P·\cos \left(\beta \right)=m·g·\cos \left(0.436\right)=1778.17 \text{N}$$ 

Donde hemos aplicado β = α' por ser sus lados perpendiculares.

A partir de aquí podemos calcular la fuerza de rozamiento, que en este caso viene dada por

$$F_r=\mu ·N=0.15·1778.17=266.72 \text{N}$$

Quedando finalmente el trabajo como

$$W={\overrightarrow{F}}_r·∆\overrightarrow{r}=F_r·∆r·\cos \left(\alpha \right)=266.72·2·\cos \left(\mathrm{\pi }\right)=\boxed{-533.44 \text{J}}$$

Por otro lado, la fuerza peso en este caso si que realiza un trabajo, ya que su componente x se encuentra en la misma dirección y sentido del movimiento.

$$P_x=P·\sin \left(\beta \right)=m·g·\sin \left(0.436\right)=829.17 \text{N}$$

$$W=\overrightarrow{P}·∆\overrightarrow{r}=P_x·∆r·\cos \left(\alpha \right)=829.17·2·\cos \left(0\right)=\boxed{1658.35 \text{J}}$$

El trabajo, en este caso es positivo, tiene el sentido del movimiento. A este tipo de trabajos también se les denomina trabajos motores.