Desplazamiento
Vector Desplazamiento
El desplazamiento de un cuerpo en un intervalo de tiempo es equivalente al cambio de su posición en ese intervalo. Dado que la posición de un cuerpo es una magnitud vectorial, el desplazamiento de un cuerpo también lo es.
donde:
- xi, xf,yi, yf, zi, zf: Coordenadas x, y y z en los puntos Pi y Pf
La unidad de medida del desplazamiento es el metro [m] y su módulo viene dado, en tres dimensiones por la siguiente expresión:
Es importante que te des cuenta que un cuerpo puede estar en movimiento entre dos instantes de tiempo y sin embargo su desplazamiento ser 0. Esto pasará siempre que las posiciones inicial y final del cuerpo en el intervalo estudiado sea la misma. En la siguiente imagen puedes ver el vector desplazamiento y los distintos conceptos presentados, en un espacio tridimensional.
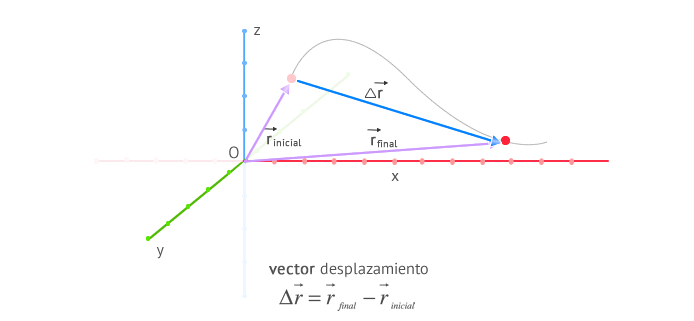
En el caso de que nos encontremos analizando el problema sólo en dos dimensiones, podemos prescindir de la coordenada z, simplificando las expresiones anteriores. El vector desplazamiento quedaría en este caso como
Y ahora... ¡Ponte a prueba!
Apartados relacionados
Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:
