Función Compuesta

La función compuesta es aquella que se obtiene mediante una operación denominada composición de funciones, que consiste en aplicar de manera sucesiva las funciones que forman parte de la operación. Así, la función compuesta de f(x) y g(x) es otra función obtenida aplicando g a las imágenes de f.

Concepto de composición de funciones

Aplicando sucesivamente la función f(x) y la función g(x) sobre los valores de x obtenemos el mismo resultado que si aplicásemos directamente una función $\left(g\circ f\right)\left(x\right)$ sobre los valores de x. A esta función se la denomina función compuesta de f y g.

En la parte inferior de la ilustración, un ejemplo concreto aplicado a x=3 con las funciones f(x)=x² y g(x)=x+2 representadas conceptualmente por dos máquinas de distintos colores.

En este apartado vamos a profundizar en el estudio de esta operación a través de los siguientes puntos:

• Definición
• Cómo se calcula
• Dominio
• Propiedades

¿Empezamos?

Definición

Observa que la función $\left(g\circ f\right)\left(x\right)$ se lee "f compuesta con g ", a pesar de ser g la primera que aparece. La razón es que es en realidad f la primera que se aplica. De manera complementaria, $\left(f\circ g\right)\left(x\right)$ se leería "g compuesta con f ".

¿Cómo se calcula?

Para realizar la composición propiamente dicha de dos funciones ilustramos el proceso con el ejemplo con el que abríamos el apartado: siendo f(x)=x² y g(x)=x+2, podemos calcular $\left(g\circ f\right)\left(x\right)$ sin más que sustituir f(x) en los lugares donde pone x en g(x), es decir:

$$\left(g\circ f\right)\left(x\right)=g\left[f\left(x\right)\right]=g\left(x^2\right)={\overline{)x+2}}_{x\Rightarrow x^2}=x^2+2$$

Observa que en general $\left(g\circ f\right)\left(x\right)\ne \left(f\circ g\right)\left(x\right)$. En el ejemplo:

$$\left(f\circ g\right)\left(x\right)=f\left[g\left(x\right)\right]=f\left(x+2\right)={\overline{)x^2}}_{x\Rightarrow x+2}={\left(x+2\right)}^2=x^2+4x+4$$

Dominio

El dominio de una función es el conjunto de valores para los cuales está definida. En el caso de la función compuesta (g ∘ f)(x), este depende de los dominios de las funciones f y g.

Observa, que al hacer g∘f, actúa en primer lugar f sobre x, y posteriormente g sobre f(x), es decir:

$$x\stackrel{f}{\to }f\left(x\right)\stackrel{g}{\to }g\left[f\left(x\right)\right]=\left(g\circ f\right)\left(x\right)$$

Por tanto, el dominio de la función compuesta debe satisfacer simultáneamente las condiciones que le imponga la primera función que actúe ($x\in Do{m}_f$), y los de la segunda, teniendo en cuenta que esta última actúa f(x) y no sobre x ($f\left(x\right)\in Do{m}_g$).

Y eso es todo, aunque podemos profundizar un poco en esta idea contándote que pueden darse dos casos:

• Que el recorrido de la primera función esté incluido en el dominio de la segunda. En este caso el dominio de la función compuesta coincide con el de la primera función.

  $$Do{m}_{g\circ f}=Do{m}_f$$

  

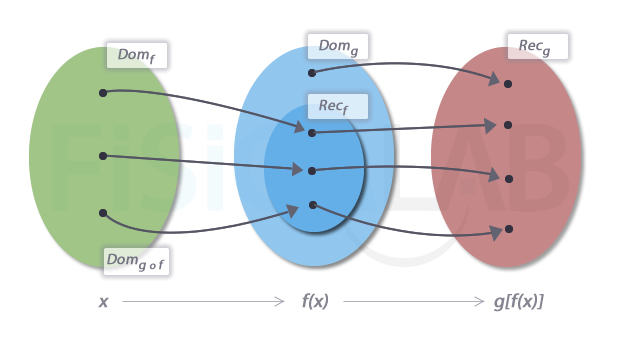
  Dominio función compuesta

  En la ilustración aparecen los dominios y recorridos de f y g. Como puedes ver, el recorrido de f está íntegramente incluido en el dominio de g, con lo que el dominio de f y de g ∘ f coinciden.

• Que el recorrido de la primera función no esté incluido en el dominio de la segunda. En este caso el dominio de la función compuesta serían aquellos valores de la primera función que son antiimagen de los valores del dominio de la segunda:

  $$Do{m}_{g\circ f}=Do{m}_f\cap f^{-1}\left(Do{m}_g\right)$$

  

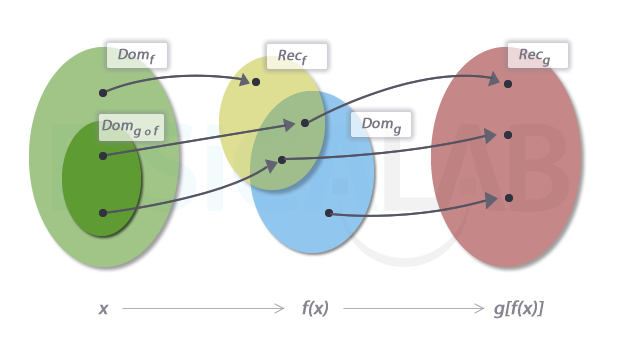
  Dominio función compuesta

  En la ilustración aparecen los dominios y recorridos de f y g. Como puedes ver, el recorrido de f no está íntegramente incluido en el dominio de g, con lo que el dominio de g ∘ f es un subconjunto de f: el de aquellos elementos que tienen imagen en el dominio de g.

En la expresión anterior aparece f^-1. Se trata de la función inversa, que vamos a estudiar en el apartado inmediatamente posterior del tema. De momento te bastará con saber que, de manera complementaria a f(x), que nos permite pasar de un valor del dominio a su imagen (que es un valor del recorrido), la función inversa f^-1(x), nos permite pasar de un valor del recorrido a su antiimagen (que es un valor del dominio).

Propiedades

• No conmutativa: $g\circ f\ne f\circ g$

  Es decir, tal y como habíamos señalado anteriormente, el orden en que aplicamos la composición generalmente condicione el resultado obtenido

• Asociativa: $h\circ \left(g\circ f\right)=\left(h\circ g\right)\circ f$

  Es decir, dadas 3 funciones cualesquiera, se obtiene igual resultado componiendo la primera (f) y la segunda (g), y componiendo posteriormente el resultado con la tercera (h), que componiendo la segunda (g) y la tercera (h) y componiendo posteriormente la primera (f) con el resultado obtenido

Por otro lado, recuerda que el elemento neutro de una operación es aquel que, al ser operado con cualquier elemento, lo deja igual, es decir, aquel que hace que la operación tenga un efecto neutro. En el caso de la composición de funciones, el elemento neutro es la función identidad I(x)=x.

$$f\circ I=I\circ f=f$$

Observa que para el caso concreto de la función identidad si se cumple la propiedad conmutativa.

Por otro lado, dada una función cualquiera f(x) y una operación (en este caso la composición de funciones), otro elemento importante es el elemento simétrico de f(x). Se trata de aquella función que, al operarse con f(x) da como resultado el elemento neutro, es decir, la función identidad en este caso. El elemento simétrico de la composición de funciones es la función inversa, que pasamos a estudiar en el siguiente apartado del tema.