Valor Absoluto de una Función

El valor absoluto de un número n es ese mismo número, cuando el número es positivo, o su opuesto cuando el número es negativo.

$$\left|n\right|=\left\{\begin{array}{ccc}n& \text{si}& n\ge 0\\ -n& \text{si}& n<0\end{array}\right.$$

Análogamente, el valor absoluto de una función se obtiene dejando la función igual, para aquellos tramos de la función que sean positivos, y cambiando su signo para aquellos tramos negativos. El ejemplo más sencillo es:

Función f(x)=|x|

$$y=f\left(x\right)=\left|x\right|=\left\{\begin{array}{ccc}x& \text{si}& x\ge 0\\ -x& \text{si}& x<0\end{array}\right.$$

En este apartado vamos a profundizar en estas ideas a través de los siguientes puntos:

• Definición
• Gráficas
• Expresión analítica

¿Empezamos?

Definición

Expresión gráfica

En una función afectada por el valor absoluto todos los valores de y deben ser positivos, por lo que su gráfica siempre quedará en la parte del semieje y positivo. De esta manera, conocida la gráfica de una función cualquiera, puedes obtener fácilmente su valor absoluto "reflejando" los tramos negativos en el eje x. Observa:

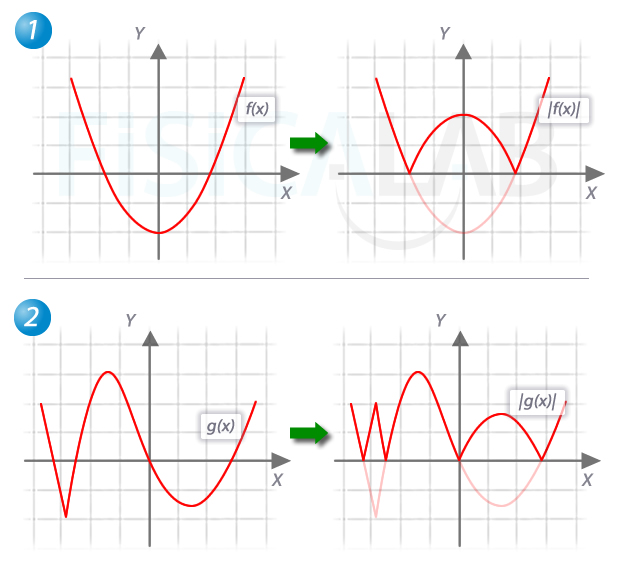
Gráficas del valor absoluto de funciones

En la ilustración, en 1 y 2 y a la izquierda, dos funciones de gráficas conocidas, f(x) y g(x). Aplicado el valor absoluto obtenemos las gráficas a la derecha. Las partes que quedaban bajo el eje x, que es la parte negativa del eje y, se "reflejan" cuando se aplica el valor absoluto, y quedan en la zona positiva de este último.

Expresión analítica

Como puedes intuir a partir de la propia definición, las funciones en valor absoluto se pueden transformar en funciones a trozos. En general, para poder representar gráficamente una función a la que se haya aplicado el valor absoluto debes comenzar transformándola en una función definida a trozos, pues así vas a poder saber los intervalos que debes "reflejar" (los negativos). Para convertir una función en valor absoluto en una función a trozos:

1. Iguala a cero la función, sin el valor absoluto, y despeja la x, es decir, calcula sus raíces
2. Las raíces forman intervalos. Evalúa el signo de la función en cada intervalo
3. Define la función a trozos teniendo presente que, en los intervalos donde la función es negativa, se cambia el signo de la misma

Recuerda, lo que debe ser positivo en el valor absoluto de una función es el valor de la misma, es decir, la f(x), o, si lo prefieres, la y. Los valores de x, en cambio, no presentan ninguna restricción adicional a la que imponga el dominio, pudiendo por tanto ser positivos o negativos.