Función Matemática

En matemáticas, cuando el valor de una magnitud depende de otra, decimos que la primera está en función de la segunda. Fue el físico y matemático suizo Leonhard Euler quien introdujo la noción de función matemática, refiriéndose a ella como f(x). En este apartado vamos a presentar el concepto de función matemática, a través de los siguientes puntos:

• Variables dependientes e independientes
• La definición de función
  • Qué es el dominio y la imagen
    • Qué es el codominio
• Representación de funciones
  • Fórmula
  • Gráfica
  • Tabla de pares ordenados
  • Algoritmo
• Conclusiones

Una vez comprendido este concepto, estarás en disposición de empezar a estudiar las funciones reales de variable real, con las que trabajaremos, sobre todo, en este nivel educativo. Pero, empecemos por el principio...

Variables independientes y dependientes

Piensa...

1. ¿De qué depende la longitud de una circunferencia?
2. ¿De qué depende la cantidad de lluvia recogida en un recipiente durante 1 hora?
3. ¿De qué depende la distancia recorrida durante un minuto por un móvil que sigue un movimiento rectilíneo uniforme?
4. ¿De qué depende el precio de la factura de la luz de tu casa?

Son ejemplos de tu día a día en los que se establecen relaciones entre distintas magnitudes. Así:

1. la longitud L de una circunferencia depende de radio R (recuerda, L = 2·π·R )
2. la cantidad de lluvia recogida durante una hora en el recipiente depende de la intensidad con la que caiga la misma (esta se suele medir en litros por metro cuadrado )
3. la distancia recorrida durante un minuto por el móvil depende de la velocidad que lleve (recuerda, s=v·t )
4. y, finalmente, el precio de la factura de la luz depende, al menos, de la cantidad de energía consumida

Observa que, en los ejemplos anteriores, existe:

• una variable independiente: el radio de la circunferencia, la intensidad con la que cae la lluvia, la velocidad del móvil o la cantidad de energía consumida de nuestros ejemplos
• una variable dependiente, que es función del valor o valores de las anteriores: la longitd de la circunferencia,, la cantidad de lluvia recogida en el recipiente, la distancia recorrida por el cuerpo o el precio final de la factura de la luz

Para expresar matemáticamente la dependencia entre variables, y poder así describir fenómenos reales, utilizamos las funciones.

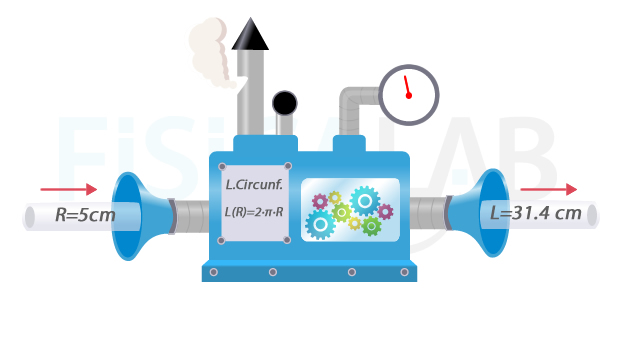
Concepto de Función

Conceptualmente puedes pensar que una función es una especie de máquina transformadora que, a partir de una variable de entrada, ofrece una salida única determinada. Así, en nuestro ejemplo de la longitud de la circunferencia, cuando la función recibe el valor del radio R (variable independiente), la "máquina" nos devuelve el valor de la longitud L (variable dependiente).

Definición

Aunque la definición anterior puede parecer bastante abstracta, no te asustes. La siguiente imagen te ayudará a aclarar estas ideas.

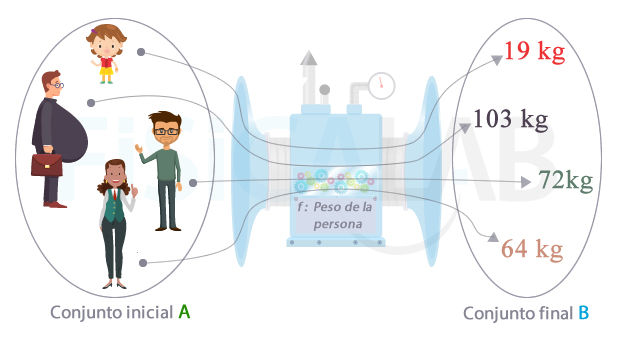
Función como relación entre conjuntos

En nuestra imagen, el conjunto A está formado por personas y el conjunto B está formado por pesos. La función f, representada por la máquina en el centro, es la encargada de asociar a cada persona su peso. Además, en la definición anterior llamábamos a a cada elemento del conjunto inicial y b a cada elemento del conjunto final. El valor de b se obtiene aplicando la regla f  "peso de la persona" al elemento a. ¿Se te ocurre qué aparato de tu día a día podría representar en este caso el funcionamiento de la máquina?

Observa que, en general, los conjuntos A y B no tienen por qué ser numéricos (en nuestro ejemplo solo el conjunto B lo es). Veamos otros ejemplos de funciones:

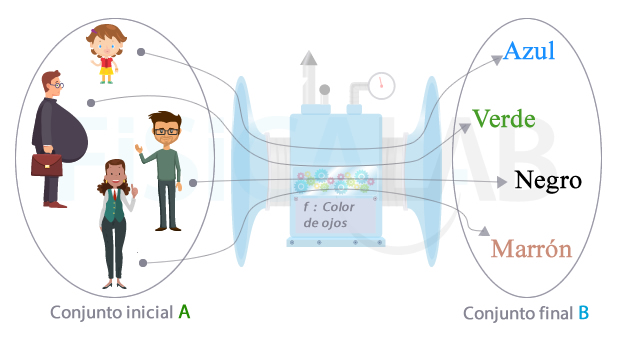
1. Una función que relaciones un conjunto A formado por personas, con un conjunto B formado por colores, a través de la regla "a cada persona su color de ojos"

   

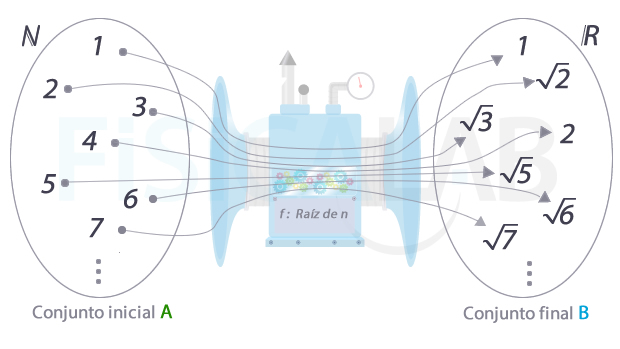
2. Una función que relaciona el conjunto A formado por los números naturales ℕ con un subconjunto de los reales ℝ tales que:

   $$\begin{array}{cccl}f:& \mathrm{\mathbb{N}}& \to & \mathrm{ℝ}\\ & n& \mapsto & y=f\left(n\right)=\sqrt{n}\end{array}\begin{array}{}\end{array}$$

   Así, al elemento n=1 les correspondería $y=\sqrt{1}$, y al elemento n=2 le correspondería $y=\sqrt{2}$.

   

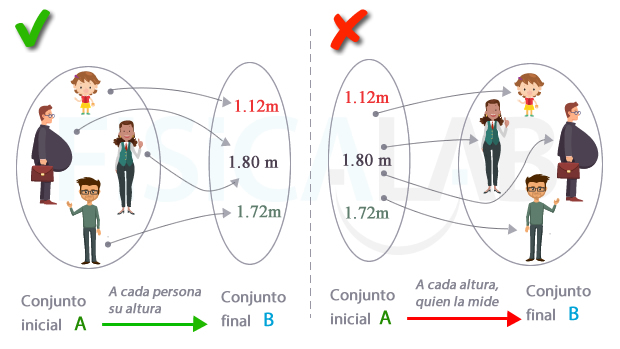
No todas las relaciones son funciones

En una función, a cada elemento de B pueden llegar varias flechas de A, pero de un elemento de A no pueden salir varias flechas. Así, dada una correspondencia que sea una función (ilustración izquierda), la correspondencia inversa (ilustración derecha) no tiene por qué serlo también.

Dominio e imagen

Así, por ejemplo:

1. El domino de la función anterior que relacionaba a cada persona con su color de ojos es el conjunto formado por las personas
2. El domino de la función que relacionaba los números naturales con su raíz cuadrada es precisamente el conjunto de números naturales ℕ

Cada elemento concreto del conjunto imagen es la imagen de algún elemento particular del conjunto dominio, que denominaremos su antiimagen. Es habitual denotar a esta imagen por y, y a su antiimagen por x. Decimos entonces que y es la imagen de x a través de f. Volviendo a nuestros ejemplos:

1. El recorrido de la función que relacionaba a cada persona con su color de ojos es el conjunto formado por los colores de ojos que realmente tienen las personas del dominio. Además, decimos que cada color de ojos concreto del conjunto imagen es la imagen de uno (o varios) elementos del dominio.

   Así, el azul es la imagen de nuestra pequeña amiga Sofía; el verde es la imagen de Carlos, el oficinista grandullón que parece no prestar demasiada atención a su dieta; El negro es la imagen de Roberto, el profe de Física de camiseta verde; y, finalmente, el marrón es la imagen de Rosa, la directora del instituto en el que trabaja Roberto, vestida también de verde.

   Por otro lado, cada persona concreta sería una antiimagen de algún color. Así Sofía es la antiimagen del azul, Carlos lo es del verde, Roberto es la antiimagen del negro y Rosa es la antiimagen del marrón.

2. El recorrido de la función que relacionaba los números naturales con su raíz cuadrada es el subconjunto de los números reales que resulta de aplicar a cada número natural su raíz cuadrada. Decimos que cada número real del conjunto imagen es la imagen de un número natural.

   Así, el 1 ( $\sqrt{1}$ ) es la imagen del 1, el $\sqrt{2}$ es la imagen del 2, el $\sqrt{3}$ es la imagen del 3, el 2 ( $\sqrt{4}$ ) es la imagen del 4 y así sucesivamente.

   Por otro lado, cada número natural concreto sería una antiimagen de algún real. Así, el 1 sería la antiimagen del 1 ($\sqrt{1}$), el 2 la antiimagen de $\sqrt{2}$ y así sucesivamente

Así, el rango depende del dominio, pero nosotros definimos el dominio cuando definimos la función. No tendría sentido aplicar la función del color de ojos vista anteriormente sobre figuras geométricas, o sobre frutas y hortalizas. El dominio debe ser un conjunto de personas.

¿Y el codominio?

Pues hasta ahora no habíamos hablado de él, pero me alegra que me hagas esa pregunta... Aunque es habitual que se confundan codominio e imagen, en realidad hay una sutil diferencia. Tan sutil que solo te recomendamos que sigas leyendo si tienes claro todos los conceptos vistos hasta aquí...

Bien... esto se parece mucho al recorrido... ¿cierto? No, no del todo. El recorrido puede coincidir con el codominio, o puede ser un subconjunto de este ( $Cod\left(f\right)\subset Rec\left(f\right)$ ). La siguiente ilustración resume estas ideas.

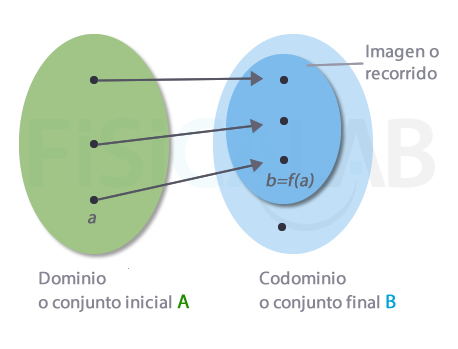
Dominio, codominio e imagen

En la ilustración tenemos una función cuyo conjunto imagen es subconjunto del codominio. Así:

• Llamamos dominio, en verde, al conjunto de valores que pueden entrar en una función.
• Llamamos codominio, en azul claro, al conjunto de valores que podrían salir de una función
• Llamamos imagen, en azul oscuro, al conjunto de valores que realmente salen de una función

Ahora que ya has entendido la diferencia entre recorrido y codominio puede que te preguntas... ¿por qué es este último importante? Simplemente porque en ocasiones no nos es posible conocer a priori el conjunto concreto de valores de salida de la función (su conjunto imagen), pero si podemos conocer los posibles valores de salida (el codominio), y así estudiar algunas propiedades de la función.

Siguiendo con nuestros ejemplos, en el caso de la función que asociaba a cada persona su color de ojos, definimos el dominio como el conjunto formado por Sofía, Carlos, Roberto y Rosa. Sin ver de cerca los ojos de nuestros amigos no podemos conocer su color, sin embargo sabemos que, sean cuales sean, serán colores (no números, ni figuras geométricas, ni frutas, ni hortalizas). Así pues, a la hora de definir nuestra función podríamos decir que su codominio es (porque así lo definimos nosotros) el conjunto formado por todos los posibles colores. Por otro lado, y como ya sabes, en este ejemplo, la imagen serían los colores azul, verde, negro y marrón.

En la función que asociaba a cada natural su raíz cuadrada, sabemos que dicho valor estará en el conjunto de los reales, pero no podemos saber a priori los valores de las infinitas raíces cuadradas de los infinitos números naturales. Así pues, a la hora de definir nuestra función podríamos decir que su codominio es (porque así lo definimos nosotros) el conjunto formado por todos los números reales, aunque su recorrido sólo sea un subconjunto de este (observa, por ejemplo, que $3.5\in Cod\left(f\right)=\mathrm{ℝ}$, pero $3.5\notin Rec\left(f\right)$ ya que no hay ningún número natural cuya raíz cuadrada de 3.5).

Representación

Una vez entendido qué son, conceptualmente, las funciones, cabe preguntarnos exactamente cómo podemos representarlas. Lo fundamental de una representación es que nos permita obtener la imagen a partir de cada elemento del dominio. Para ello se proporciona una regla de transformación o de correspondencia, que puede estar dada en distintas formas.

Fórmula o ecuación matemática

Damos la regla de correspondencia mediante una fórmula que relaciona algebraicamente varias magnitudes. Implica que tanto el conjunto inicial como el final son numéricos, normalmente números reales.

• $f\left(x\right)=5x+2$; Se lee "efe de equis igual a cinco equis más dos". En azul hemos marcado el valor de entrada a la función, en verde el valor de salida, y la regla de transformación sería 5·x+2

• $y=5·x+2$; En este caso al valor de salida lo llamamos y

• $g\left(x\right)=\frac{5·x+2}{2^x}$; La particularidad esta vez es que la llamamos g, en lugar de f

• $\text{altura de Alejandro}\left(t\right)=\left\{\begin{array}{ll}50& \text{si} 0⩽t<3\\ 50·\left(t-2\right)& \text{si} 3\le t<18\end{array}\right.$; En esta ocasión a la variable independiente la hemos llamado t; a la función, "Altura de Alejandro". Se trata de una función definida a trozos

• ${\overrightarrow{F}}_g\left(r\right)=-G·\frac{M·m}{r^2}·{\overrightarrow{u}}_r$; Se trata de la fórmula de la fuerza gravitacional con la que se atraen dos cuerpos. En este caso el valor de salida es un vector, y el de entrada lo hemos llamado r, que representa la distancia que separa dos cuerpos. Observa que, aunque aparezcan varias letras, la única variable independiente es r, que es la que aparece como ${\overrightarrow{F}}_g\left(r\right)$ . El resto de elementos de la ecuación se consideran constantes para dos cuerpos determinados

Cuando queremos ser más precisos e indicar exactamente el dominio y el codominio de la función, utilizamos la notación:

$$\begin{array}{cccl}f:& \mathrm{\mathbb{N}}& \to & \mathrm{ℝ}\\ & x& \to & y=f\left(x\right)=\sqrt{x}\end{array}\begin{array}{}\end{array}$$

Que también podrás ver como...

$$\begin{array}{cccl}f:& \mathrm{\mathbb{N}}& \to & \mathrm{ℝ}\\ & x& \mapsto & \sqrt{x}\end{array}\begin{array}{}\end{array}$$

Tablas de pares ordenados

A cada pareja de valores entrada-salida correspondientes se le denomina par ordenado y se suele denotar por (x, f(x)). En ocasiones, sólo son relevantes ciertos valores de la función. Podemos formar una tabla a partir de ellos, con los pares ordenados en la forma:

Por ejemplo, podemos representar los valores de velocidad de un móvil durante los 3 primeros segundos de su recorrido:

A partir de estos datos, ¿sabrías decir de qué tipo de movimiento se trata?

Gráfica

Otra forma muy habitual de dar la regla de correspondencia es mediante una gráfica. Cuenta con unos ejes (habitualmente los ejes cartesianos) que representan las variables de entrada (independientes) y salida (dependientes). Sobre ellos se dibujan los puntos correspondientes a los pares ordenados en el lugar del plano (o del espacio, en el caso de funciones reales de dos variables independientes) que les corresponda. Uniendo estos puntos nos queda un trazo lineal (o una superficie) que representa la función buscada.

Las gráficas son ideales para visualizar y conocer intuitivamente algunas características de las funciones estudiadas, tales como su crecimiento, decrecimiento, máximos, mínimos, etc. Algunos ejemplos:

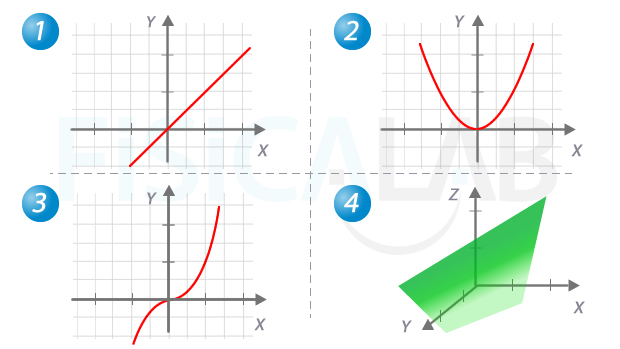
Gráficas de funciones

En la ilustración puedes ver 4 gráficas de funciones representadas sobre los ejes cartesianos. La 1 se corresponde a la función f(x)=x, la segunda f(x)=x². La tercera f(x)=x³. La cuarta corresponde a una función de dos variables f(x,y)=x+y, con lo que su gráfica es una superficie en el espacio.

Algoritmo

Aunque menos habitual en este nivel educativo, también es posible expresar las funciones matemáticas "explicando" la regla de correspondencia. Por ejemplo:

• multiplica el número por dos,
• obtén la última letra de la palabra o...
• ... encuentra el primer número primo mayor que el número natural dado

Existen numerosos lenguajes formales para expresar esta "explicación", que denominamos algoritmo, los conjuntos de valores sobre los que puede actuar (ya sabes, el dominio) y los valores que se podrían obtener como salida (el codominio). Los lenguajes de programación son una buena muestra de ello.

Observa este ejemplo, en el que expresamos la regla "obtén la última letra de la palabra" de una manera formal. Para ello convenimos que el dominio sea el conjunto de palabras del castellano, P={Palabras del castellano} , y el codominio el conjunto de letras del castellano L={Letras del castellano}. Así, la regla de correspondencia vendrá dada por:

$$\begin{array}{cccl}f:& P& \to & L\\ & p& \mapsto & \text{letra final de }p\end{array}\begin{array}{}\end{array}$$

Conclusión

En este apartado hemos estudiado el concepto de función matemática y los elementos que la componen. A lo largo del resto del tema vamos a presentar y estudiar en profundidad las funciones reales de variable real. Practicaremos ejercicios con ellas, aprenderemos a estudiar sus características, a representarlas gráficamente y a ver sus usos en Física. Visita el resto de apartados del tema para continuar aprendiendo sobre este importante concepto matemático.