Gravedad y masas en vértices de cuadrado

Enunciado

dificultad

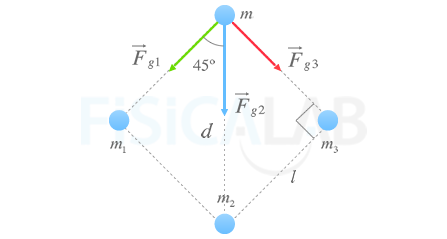
En los vértices de un cuadrado de lado l, como el de la figura, se sitúan 4 masas. Determina la aceleración de la masa m sujeta a la acción de las otras tres. ¿Qué valores deben tener las masas para que la masa m estudiada se desplace sólo en sentido vertical?

cuatro masas situadas en los vértices de un cuadrado de lado l

Solución

Datos

La propia imagen contiene todos los datos necesarios para la resolución del problema.

Resolución

Podemos dibujar, sobre la imagen de la figura, las tres fuerzas que actúan sobre la masa m, cada una de ellas debida a la presencia de una masa. Además, situaremos el origen de coordenadas tal y como se indica en la figura, y pondremos de relevancia el hecho de que la diagonal del cuadrado, d, es la hipotenusa de un triángulo rectángulo cuyos catetos valen l.

cuatro masas y las fuerzas de gravitación que sufre una de ellas

A partir de la segunda ley de Newton, podemos escribir:

${\vec{F}}_{T} = m \cdot \vec{a}$

La fuerza total que actúa sobre la masa vendrá dada por la suma vectorial de cada fuerza que actúa por separado:

${\vec{F}}_{T} = {\vec{F}}_{g_{1}} + {\vec{F}}_{g_{2}} + {\vec{F}}_{g_{3}}$

Comenzaremos calculando los módulos de cada fuerza, a partir de la expresión general del módulo de la ley de la gravedad para dos masas cualesquiera m y M, $F_{g} = G \cdot \frac{M \cdot m}{r^{2}}$

$F_{g_{1}} = G \cdot \frac{m \cdot m_{1}}{l^{2}}; F_{g_{3}} = G \cdot \frac{m \cdot m_{3}}{l^{2}}$

Para el caso de la segunda masa m₂, debemos determinar la distancia de separación en función del lado l. Esto es, la diagonal del cuadrado, d:

$d^{2} = l^{2} + l^{2} \Rightarrow d = \sqrt{2} \cdot l$

A partir de aquí, podemos escribir:

$F_{g_{2}} = G \cdot \frac{m \cdot m_{2}}{{(\sqrt{2} \cdot l)}^{2}} = G \cdot \frac{m \cdot m_{2}}{2 \cdot l^{2}}$

Por otro lado, podemos dar la expresión vectorial de estas fuerzas a partir de sus módulos y del vector unitario que las define, que podemos determinar a partir de la figura anterior, quedando:

${\vec{u}}_{r_{1}} = - \cos (45 º) \cdot \vec{i} - \sin (45 º) \cdot \vec{j} \Rightarrow {\vec{F}}_{g_{1}} = F_{g_{1}} \cdot {\vec{u}}_{r_{1}} {\vec{u}}_{r_{2}} = - \vec{j} \Rightarrow {\vec{F}}_{g_{2}} = F_{g_{2}} \cdot {\vec{u}}_{r_{2}} {\vec{u}}_{r_{3}} = \cos (45 º) \cdot \vec{i} - \sin (45 º) \cdot \vec{j} \Rightarrow {\vec{F}}_{g_{3}} = F_{g_{3}} \cdot {\vec{u}}_{r_{3}}$

Finalmente, podemos escribir:

${\vec{F}}_{T} = {\vec{F}}_{g_{1}} + {\vec{F}}_{g_{2}} + {\vec{F}}_{g_{3}} = G \cdot \frac{m}{l^{2}} (m_{1} \cdot (- \cos (45 º) \cdot \vec{i} - \sin (45 º) \cdot \vec{j}) + \frac{m_{2}}{2} \cdot (- \vec{j}) + m_{3} \cdot (\cos (45 º) \cdot \vec{i} - \sin (45 º) \cdot \vec{j})) = = G \cdot \frac{m}{l^{2}} \cdot (\frac{\sqrt{2}}{2} \cdot (m_{3} - m_{1}) \cdot \vec{i} - (\frac{m_{2}}{2} + \frac{\sqrt{2}}{2} \cdot (m_{1} + m_{3})) \cdot \vec{j})$

Finalmente, podemos considerar despejar la aceleración de la expresión de la segunda ley de Newton o principio fundamental, quedando:

$\vec{a} = \frac{{\vec{F}}_{T}}{m} \Rightarrow \vec{a} = G \cdot \frac{1}{l^{2}} \cdot (\frac{\sqrt{2}}{2} \cdot (m_{3} - m_{1}) \cdot \vec{i} - (\frac{m_{2}}{2} + \frac{\sqrt{2}}{2} \cdot (m_{1} + m_{3})) \cdot \vec{j}) m / s^{2}$

A partir de la expresión anterior, resulta evidente que si m₁ = m₃, la aceleración sólo tendrá componente vertical y por tanto el cuerpo no se desplazará horizontalmente.

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Fórmulas

Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.

Fórmulas

Apartados relacionados