Límites de funciones racionales en un punto
Enunciado
Resuelve, cuando sea posible, los límites de las funciones racionales siguientes, e interpreta el resultado graficamente:
- El límite de la función
Solución
Consideraciones previas
Recuerda que para resolver un límite de una función en un punto siempre comenzamos sustituyendo la x por el valor al que tiende. En el caso de las funciones racionales podemos encontrarnos 3 casos:
- Que no se anule el denominador. Entonces el resultado obtenido es directamente el límite, ya que la función es continua en el punto pedido
- Que se anule el denominador pero no el denominador. Entonces hay que calcular los límites laterales, pues aunque el valor al que tiende la x no está en el dominio, si lo están los valores próximos a él.
- Que se anulen numerador y denominador. Esto puede indicar, en el caso de los cocientes de polinomios como los aquí resueltos, la presencia de un factor común que habrá que simplificar.
Te recomendamos que estudies la teoría asociada si aún no lo has hecho.
Resolución
1.-
En este primer caso, nos encontramos ante una función racional que no se anula ni en el denominador ni en el numerador. Se trata de una función continua en x=3, con lo que el límite se obtiene de manera directa.
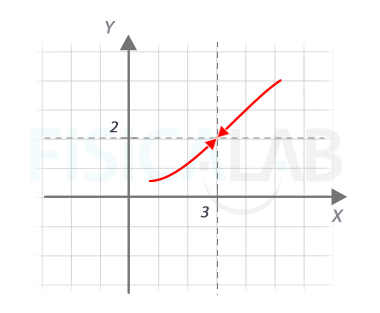
Interpretación gráfica
Gráficamente vemos que, a medida que nos acercamos al x=3, tanto por la izquierda como por la derecha, la función se acerca a y=2, el valor del límite.
2.-
Puesto que se anula el numerador, pero no el denominador, se trataría en realidad del mismo caso del apartado 1.
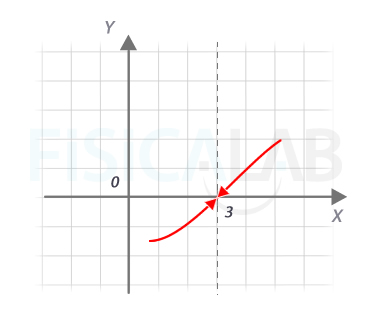
Interpretación gráfica
Gráficamente vemos que, a medida que nos acercamos al x=3, tanto por la izquierda como por la derecha, la función se acerca a y=0, el valor del límite. De nuevo, la función es continua en ese punto.
3.-
Se trata de una indeterminación del tipo k/0. Veamos qué ocurre con los límites laterales:
Por un lado, observa que en el numerador no es relevante el lateral por el que nos acerquemos a -1, sólo lo es en el denominador, al cambiar el signo de 0- y 0+. Por otro, los límites laterales son distintos, con lo que diremos que no existe el límite:
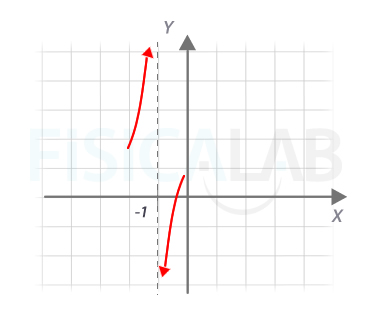
Interpretación gráfica
Gráficamente vemos que, a medida que nos acercamos al x=-1 por la izquierda, la función se va a infinito, y si lo hacemos por la derecha la función se va a menos infinito. x=-1 es una asíntota vertical.
Recuerda, por otro lado, que algunos autores prefieren escribir directamente
4.-
En este caso debemos factorizar numerador y denominador. El caso del denominador es inmediato. El del numerador, podemos buscar las raíces de x2-1, pero es más rápido acordar que "suma por diferencia es igual a diferencia de cuadrados", esto es: x2-1=(x+1)·(x-1). Con lo que nos queda:
Debemos calcular ahora los límites laterales:
Con lo que no existe el límite:
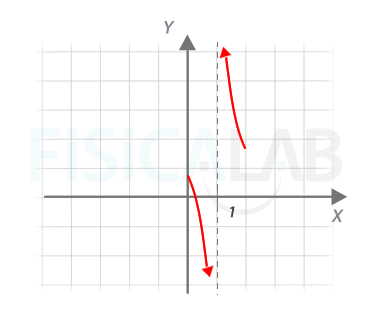
Interpretación gráfica
Gráficamente vemos que, a medida que nos acercamos al x=1 por la izquierda la función se va a menos infinito, y si lo hacemos por la derecha la función se va a infinito. La recta x=1 es una asíntota vertical.
5.-
Calculemos los límites laterales:
Con lo que esta vez si existe el límite, y vale:
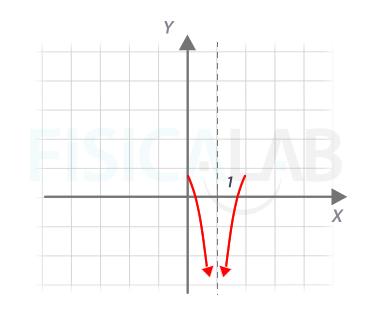
Interpretación gráfica
Gráficamente vemos que, a medida que nos acercamos al x=1 tanto por la izquierda como por la derecha, la función se va a menos infinito. Por eso decimos que existe el límite, porque los dos laterales coinciden. Además, la recta x=1 es una asíntota vertical.
6.-
Hemos obtenido, una vez más, una operación indeterminada. Podemos factorizar numerador y denominador:
Respecto al denominador:
Así pues, reescribiendo nuestro límite nos queda:
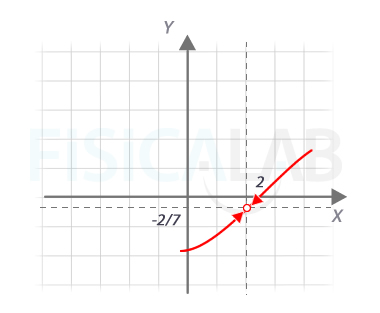
Interpretación gráfica
Gráficamente vemos que, a medida que nos acercamos al x=2 la función se aproximaría al valor del límite, -2/7. Sin embargo, dado que en x=2 se anula el denominador, la función no está definida.
7.1.-
Calculando los límites laterales tenemos:
Con lo que no existe el límite:
7.2.-
Como ves, sencillo y directo.
7.3.-
Calculando los límites laterales nos queda esta vez:
Con lo que, de nuevo, no existe el límite:
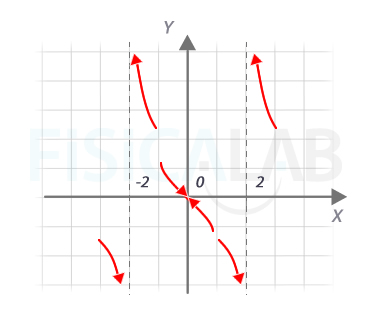
Interpretación gráfica
Gráficamente vemos que, hay dos asíntotas verticales, en las que la función diverge: son x=-2 y x=2. Por otro lado, en x=0 la función es contínua.
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
