Representación de funciones con valor absoluto

Consideraciones previas

Para representar gráficamente las funciones dadas, todas ellas con valor absoluto, comenzaremos por la representación de las mismas sin el valor absoluto. Posteriormente hayamos los puntos de corte de la función con el eje x (puntos que hacen y=0), y reflejamos sobre el eje x todo lo que quede en la parte negativa del eje y.

Para convertirlas en funciones a trozos debemos utilizar los puntos de corte con el eje x, pues son los puntos en los que la función puede cambiar de signo. Estos puntos determinan intervalos en los que el signo de la función permanece constante y son los puntos de cambio de rama en la función definida a trozos equivalente. Aquellos intervalos de signo negativo deben ser "reflejados" analíticamente, es decir, en ellos la función se multiplica por -. El estudio del signo se cede hacer bien con una tabla, como en este ejercicio, o bien estudiando la gráfica, como haremos aquí.

Resolución

$$\boxed{f\left(x\right)=\left|\frac{3x}{2}-1\right|}$$

Si prescindimos del valor absoluto, tal como hemos indicado, se trata de la ecuación de una recta en la forma f(x)=y=ax+b. Dando dos valores cualesquiera a la variable independiente x podemos obtener los valores de y correspondientes. Usando una tabla de valores:

$$y=\frac{3x}{2}-1\Rightarrow \begin{array}{cc}x& y\\ 0& \frac{3·0}{2}-1=-1\\ 2& \frac{3·2}{2}-1=2\end{array}$$

Ahora ya estamos en disposición de representar la función sin valor absoluto:

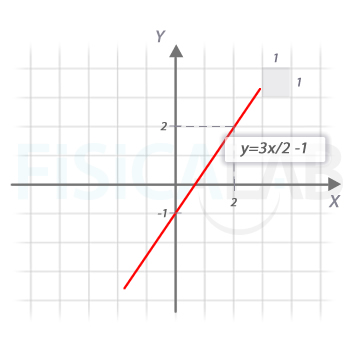
Aunque nos bastaría reflejar la parte negativa de la función para obtener la representación de la función original en valor absoluto, buscaremos de manera analítica los puntos de corte a fin de señalarlos en el eje x en la representación final.

$$0=\frac{3x}{2}-1\Rightarrow x=\frac{2}{3}$$

Con lo que la gráfica final pedida nos queda:

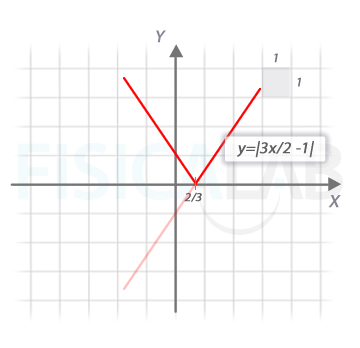
La función a trozos nos queda:

$$f\left(x\right)=\left\{\begin{array}{ccc}-\frac{3x}{2}+1& \text{si}& x<\frac{2}{3}\\ \frac{3x}{2}-1& \text{si}& x\ge \frac{2}{3}\end{array}\right.$$

Ten presente que el signo igual puede ir en cualquiera de las ramas.

$$\boxed{f\left(x\right)=\left|x^2+2x-2\right|}$$

En este caso nos encontramos ante una parábola en la forma y=a·x²+b·x+c afectada por el valor absoluto. Dado que a>0, las ramas de la parábola están hacia arriba, el vértice se encuentra en:

$$x_v=\frac{-b}{2·a}=\frac{-2}{2}=-1\Rightarrow y_v=f\left(x_v\right)=f\left(-1\right)=-3$$

Nos resultará de utilidad para la representación de la función sin valorar absoluto buscar ya los puntos de corte con el eje x.

$$x^2+2x-2=0\Rightarrow x=\frac{-2\pm \sqrt{2^2-4·1·\left(-2\right)}}{2·1}=\left\{\begin{array}{l}{x}_1=\frac{-2+\sqrt{12}}{2}=0.73\\ x_2=\frac{-2-\sqrt{12}}{2}=-2.73\end{array}\right.$$

Ya podemos representar a la función, tanto sin valor absoluto como con él:

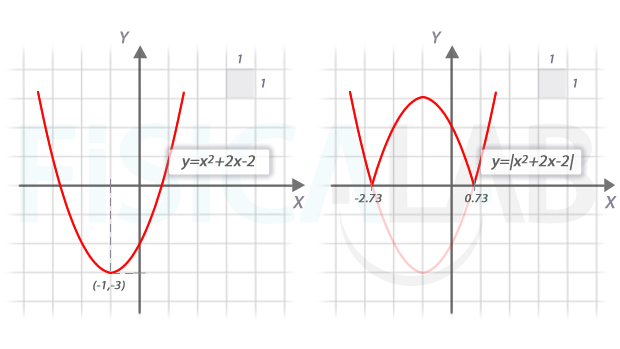
En cuanto a la función a trozos quedaría:

$$f\left(x\right)=\left\{\begin{array}{ccc}{x}^2+2x-2& \text{si}& x<-2.73\\ -x^2-2x+2& \text{si}& -2.73\le x\le 0.73\\ x^2+2x-2& \text{si}& x>0.73\end{array}\right.$$

$$\boxed{f\left(x\right)=\left|-x^2-2x+2\right|}$$

Observa que la parábola en el interior del valor absoluto coincide con la del apartado anterior cambiada de signo, es decir, con las ramas hacia abajo. Los puntos de corte con el eje x son los mismos, y el vértice tiene la misma coordenada x, aunque opuesta coordenada y. De manera que la representación final queda:

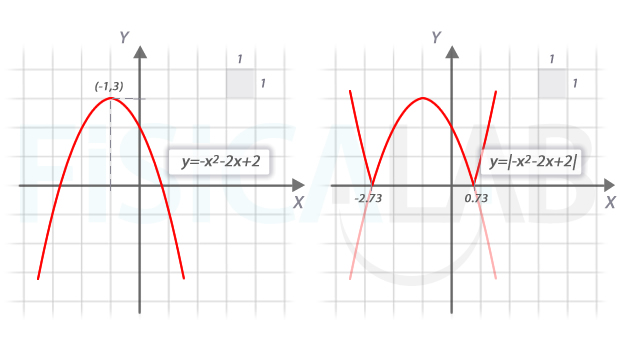
La representación por ramas nos queda:

$$f\left(x\right)=\left\{\begin{array}{ccc}{x}^2+2x-2& \text{si}& x<-2.73\\ -x^2-2x+2& \text{si}& -2.73\le x\le 0.73\\ x^2+2x-2& \text{si}& x>0.73\end{array}\right.$$

Como puedes observar, tanto la representación gráfica como la analítica a trozos coinciden con la del apartado anterior.

$$\boxed{f\left(x\right)=\left|e^x-1\right|}$$

En este caso se trata de una función exponencial, que ha sufrido una transformación desplazándola una unidad verticalmente hacia abajo. Recuerda que la función exponencial de base e pasa por (0,1) y (1,e).

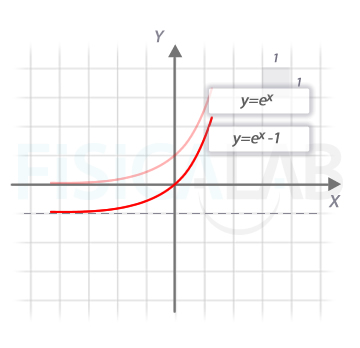
Ahora buscamos analíticamente el punto/los puntos en los que se corta el eje x para poder hacer la reflexión vertical de manera precisa:

$$\begin{gathered} e^x-1=0\Rightarrow e^x=1\underset{\ln \left(\right)=\ln \left(\right)}{\Rightarrow }\ln \left(e^x\right)=\ln \left(1\right)\underset{\ln \left(a^b\right)=b\ln \left(a\right)}{\Rightarrow }x\ln \left(e\right)=\ln \left(1\right)\underset{\ln \left(e\right)=1 \\ \ln \left(1\right)=0}{\Rightarrow }x=0 \end{gathered}$$

Con lo que la representación final nos queda:

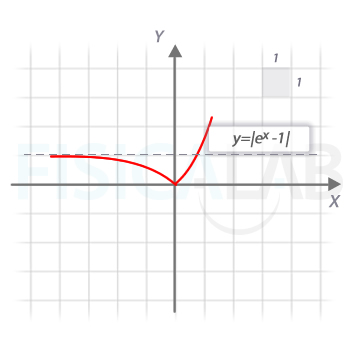
La función por ramas queda:

$$f\left(x\right)=\left\{\begin{array}{ccc}-e^x+1& \text{si}& x<0\\ e^x-1& \text{si}& x\ge 0\end{array}\right.$$

$$\boxed{f\left(x\right)=\left|\ln \left(x\right)\right|}$$

Sabemos que la función logaritmo de x tiene la forma:

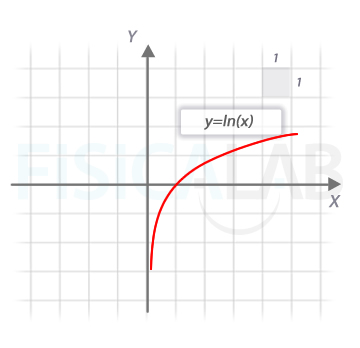
Buscando analíticamente el punto de corte con el eje x tenemos:

$$\ln \left(x\right)=0\Rightarrow x=1$$

Con lo que la función final nos queda:

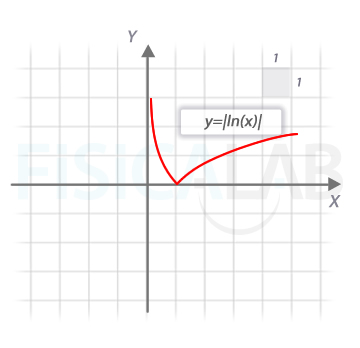
En cuanto a la forma por ramas:

$$f\left(x\right)=\left\{\begin{array}{ccc}-\ln \left(x\right)& \text{si}& x<1\\ \ln \left(x\right)& \text{si}& x\ge 1\end{array}\right.$$