The english physicist, mathematician and astronomer Sir Isaac Newton (1642-1727), basen on the studies of Galileo and Descartes, published in 1684 the first great work in Physics: Philosophiæ Naturalis Principia Mathematica, also known as Principia. In the first of the three parts in which the work is divided, he exposes in three laws of motion the relations between forces and their dynamic effects: the laws of motion.
- Newton´s first law or inertia principle
- Newton´s second law or law of force and acceleration
- Newton´s third law or law of action and reaction.
Newton´s second law or fundamental principle establishes that the accelerations a body experiments are proportional in relation to the forces it receives. Probably its most famous form is:
In this chapter we are going in depth in its study, and we will see that the previous one, very useful though, is not its general form. We will follow the next points:
- Concept
- Definition
- We generalize through the diferential definition.
- We go into details in the case the mass remains unaltered
- Newton´s definition
Let´s get started!
Concept
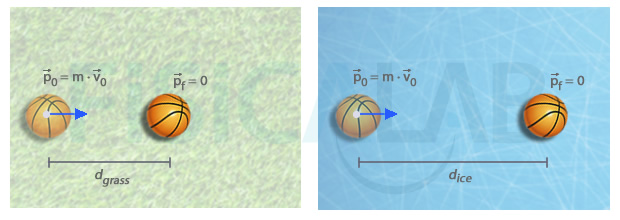
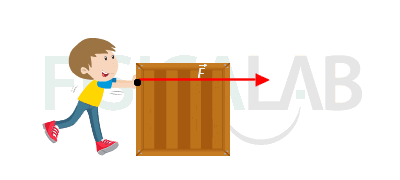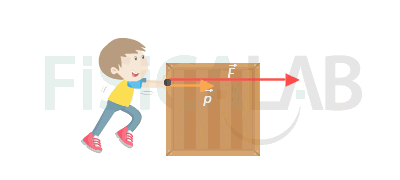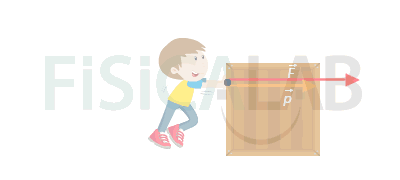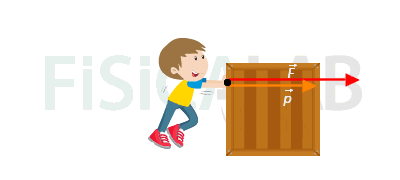
Imagine two bodies, A and B, same mass and they move at the same velocity on different horizontal surfaces. After a while, A stops and later on B stops. The two have the same initial linear momentum, A loses it before B though. So, we can guess that the interaction´s intensity between the bodies and the ground, which makes the bodies end up stopping, is higher in A than in B.
So, if we say that the force is the intensity of the interaction, we get to the definition of the Newton´s second law.
Definition
Newton´s second law or law of force and acceleration establishes a relationship between the force F acting on a body of mass m and the acceleration a caused by this force:
Where:
- Δt : Represents the considered time interval. Unit of measure: s (second).
As you can see, this principle relates mathematically the forces with the effect they produce, since it is essential in order to resolve any problem regarding dynamics.
Diferential Definition
On the previous expression we are taking for granted that the total force is constant at the interval Δt. Generally, forces are not equalduring the whole time interval, so it will be very useful an ecuation that determine the force at a concrete instant of time.
We can obtain the instantaneous total force by calculating the force between two instants of time very close to each other that their interval tends to 0. It is the definition of derivative and the same process we followed at the case of instantaneous velocity or instantaneous acceleration:
The resultant force acting on a body at an instant is proportional to the variation of the linear momentum at that precise instant and acts on the direction of this, this is the direction of the variation of its velocity.
Bear in mind that the Newton´s second law is only valid on inertial reference frames. For non inertial reference systems is necessary to include the fictitious forces or inertial forces.
Unaltered Mass
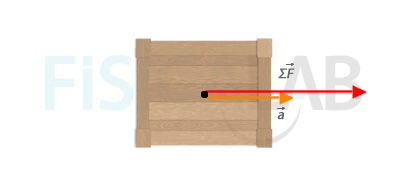
If a body does not change the value of its mass during an interaction, we obtain the famous equation we studied previously: F = m · a. Let´s see it:
We know the previous expression as fundamental equation of translational dynamics.
Fundamental equation of translational dynamics establishes that should the resultant force exerted on a free body is not invalid, this will experiment an acceleration or a change in its state at rest or state of motion.
Where:
- m : It is the mass of a body, supposedly constant. Unit of measure is kilogram (kg)
Occasionally we will find very useful to decompose the previous expression into the cartesian components (or any other coordinate system)...
Sometimes in the intrinsic components also.
On the other hand, Newton will get into this conclusion after making a series of experiments where he could check that:
- Should the same force is exerted on bodies with different mass, different accelerations are obtained.
- The force is directly proportional to the acceleration the body experiments, and the constant of proportionality of the body given corresponds to its mass.
In Newton´s first law the inertia concept was introduced, so, in the second law he establishes what is its quantity, the mass is the magnitude that measures the amount of inertia a body owns.
Observe that we can consider Newton´s first law as a particular case on this second law. Indeed...
...if there is no net force acting on a body, it does not vary its quantity of motion, so, its velocity remains constant. This is the principle of conservation of linear momentum.
Newton´s second law provides us a relation among causes, forces and effects, acceleration...It does not say anything about which factors affect on those causes. So, for instance, gravity force depends on masses and distances. Elastic force depends on the characteristics of the spring and the stretch. We will study some of these causes and applications in the next subject.
Newton´s definition
Newton´s second law allow us to define the unit on the S.I, the newton
A newton is defined as a unit of force that will accelerate one kilogram of mass one meter per second squared. Abbreviation N.
1 N = 1kg·1m/s2