Cálculo de asíntotas

Consideraciones previas

Como se trata de funciones racionales:

• Los denominadores que se anulan (sin raíces comunes en el numerador) nos darán las asíntotas verticales, cuya ecuación será x=a
• Los límites en infinito y menos infinito nos darán las asíntotas verticales, cuando de ellos obtengamos un valor real concreto. La ecuación será, en este caso, en la forma y=k
• Si el grado del numerador es una unidad superior al del denominador, dividiendo obtenemos un cociente que es un polinomio de grado 1, que es precisamente la asíntota oblicua en la forma y=ax+b

Resolución

1.-

$$\boxed{f\left(x\right)=\frac{2-4x^2}{x^2-1}}$$

Comenzamos por las asíntotas verticales:

$$\text{A.V.} x^2-1=0\Rightarrow \left\{\begin{array}{l}{x}_1=1\\ x_2 = -1\end{array}\right.$$

Por tanto, hay dos asíntotas verticales x=1 y x=-1. Efectivamente:

$$\begin{array}{c}\underset{x\to 1}{\lim }\frac{1-2x^2}{x^2-1}=\frac{-1}{0}=\infty \\ \underset{x\to -1}{\lim }\frac{1-2x^2}{x^2-1}=\frac{-1}{0}=\infty \end{array}$$

Observa que, estrictamente hablando, -1/0 es una indeterminación de tipo k/0 que habría que resolver mediante los límites laterales para saber la posición de la curva respecto a la asíntota. Así pues:

$$\begin{gathered} \begin{array}{c}\underset{x\to 1^{-}}{\lim }\frac{1-2x^2}{x^2-1}=\frac{-1}{0^{-}}=\infty \\ \underset{x\to 1^{+}}{\lim }\frac{1-2x^2}{x^2-1}=\frac{-1}{0^{+}}=-\infty \end{array} \\ \begin{array}{c}\underset{x\to -1^{-}}{\lim }\frac{1-2x^2}{x^2-1}=\frac{-1}{0^{+}}=-\infty \\ \underset{x\to -1^{+}}{\lim }\frac{1-2x^2}{x^2-1}=\frac{-1}{0^{-}}=\infty \end{array} \end{gathered}$$

Respecto a las asíntotas horizontales...

$$\begin{gathered} \underset{x\to \infty }{\lim }\frac{2-4x^2}{x^2-1}\underset{\text{Por comparación de infinitos}}{=}-4 \\ \underset{x\to -\infty }{\lim }\frac{2-4x^2}{x^2-1}=\underset{x\to \infty }{\lim }\frac{2-4{\left(-x\right)}^2}{{\left(-x\right)}^2-1}=\underset{x\to \infty }{\lim }\frac{2-4x^2}{x^2-1}\underset{\text{Por comparación de infinitos}}{=}-4 \end{gathered}$$

Por tanto, la asíntota horizontal tiene ecuación y=-4. Para saber si la curva se aproxima a la curva desde arriba o desde abajo, damos un valor muy grande a la x (positivo o negativo) y vemos si la imagen correspondiente de la función es mayor o menor que -4. Veamos:

$$\begin{gathered} f\left(50\right)=\frac{2-4x^2}{x^2-1}=-4.001<-4 \\ f\left(-50\right)=\frac{2-4x^2}{x^2-1}=-4.001<-4 \end{gathered}$$

Así pues, la curva se aproxima a la asíntota desde abajo, tanto en infinito como en menos infinito.

Por otro lado, como los límites en infinito y en menos infinito dan un valor concreto, no hay asíntotas oblicuas, ya que estas exigen que el límite sea infinito (o menos infinito). Con todos los datos anteriores ya estamos en disposición de situar la curva respecto a las asíntotas:

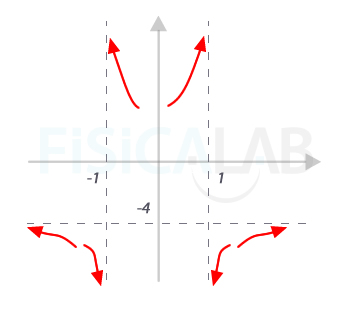
2.-

$$\boxed{f\left(x\right)=\frac{x^2+2}{x^3}}$$

Comenzamos con las asíntotas verticales:

$$x^3=0\Rightarrow x=0$$

Por tanto, la ecuación de la asíntota vertical es x=0:

$$\underset{x\to 0}{\lim }\frac{x^2+2}{x^3}=\frac{2}{0}=\infty$$

Para situar la curva respecto a ella, calculamos los límites laterales:

$$\begin{gathered} \underset{x\to 0^{-}}{\lim }\frac{x^2+2}{x^3}=\frac{2}{0^{-}}=-\infty \\ \underset{x\to 0^{+}}{\lim }\frac{x^2+2}{x^3}=\frac{2}{0^{+}}=\infty \end{gathered}$$

Por la izquierda se va a menos infinito y por la derecha a infinito.

Respecto a las horizontales:

$$\begin{gathered} \underset{x\to \infty }{\lim }\frac{x^2+2}{x^3}\underset{\text{Por comp. inf.}}{=}0 \\ \underset{x\to -\infty }{\lim }\frac{x^2+2}{x^3}=\underset{x\to \infty }{\lim }\frac{x^2+2}{-x^3}\underset{\text{Por comp. inf.}}{=}0 \end{gathered}$$

Con lo que la ecuación de la asíntota horizontal es y=0.

Para saber si la función se acerca desde arriba o desde abajo a la asíntota seguimos el procedimiento del apartado anterior:

$$\begin{gathered} f\left(50\right)=0.02 >0 \\ f\left(-50\right)=-0.02 <0 \end{gathered}$$

Es decir, la curva se acerca por arriba de la asíntota horizontal en infinito y por abajo en menos infinito.

Finalmente, como los límites en infinito y en menos infinito dan un valor concreto, no hay asíntotas oblicuas, ya que estas exigen que el límite sea infinito (o menos infinito). Con todos lo datos anteriores podemos hacer el esbozo de las posiciones de la curva respecto a las asíntotas:

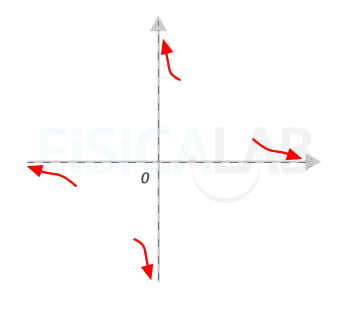
3.-

$$\boxed{f\left(x\right)=\frac{x^2-4}{x+1}}$$

Empezamos por las asíntotas verticales:

$$x+1=0\Rightarrow x=-1$$

La asíntota vertical, tiene por ecuación x=-1. Para saber la posición de la curva respecto a la misma:

$$\begin{gathered} \underset{x\to -1^{-}}{\lim }\frac{x^2-4}{x+1}=\frac{-3}{0^{-}}=\infty \\ \underset{x\to -1^{+}}{\lim }\frac{x^2-4}{x+1}=\frac{-3}{0^{+}}=-\infty \end{gathered}$$

Es decir, a la izquierda de la asíntota la curva se va a infinito y a la derecha a menos infinito. Respecto a las asíntotas horizontales, no existen, ni por la derecha (x→+∞) ni por la izquierda (x→-∞), pues:

$$\begin{gathered} \underset{x\to \infty }{\lim }\frac{x^2-4}{x+1}=\infty \Rightarrow \nexists \text{Asíntota horizontal derecha} \\ \underset{x\to -\infty }{\lim }\frac{x^2-4}{x+1}=\underset{x\to \infty }{\lim }\frac{x^2-4}{-x+1}=-\infty \Rightarrow \nexists \text{Asíntota horizontal izquierda} \end{gathered}$$

Sin embargo, sí que podemos encontrar asíntota oblicua:

$$\left.\begin{array}{r}\text{Grado}\left(x^2-4\right)=2 \\ \text{Grado}\left(x+1\right)=1\end{array}\right\}2-1=1\Rightarrow \text{Asíntota Oblicua}$$

Dividiendo:

$$\frac{x^2-4}{x+1}=\mathit{x}\mathbf{-}\mathbf{1}-\frac{3}{x+1}$$

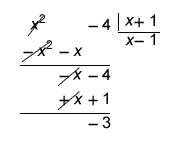
Por tanto, la ecuación de la asíntota es y=x-1. Para saber si la función se aproxima por encima o por debajo a la gráfica podemos dar un valor alto a la función de la ecuación y a la propia función y ver cual es superior, o bien determinar el valor de $-\frac{3}{x+1}$ para valores altos de x. Así, para valores altos de x, -3/(x+1) resta a la asíntota, por tanto la curva quedará por debajo. Para valores muy negativos, suma, con lo que la curva quedará por encima de la asíntota. Con todos estos datos ya estamos en disposición de realizar el esbozo:

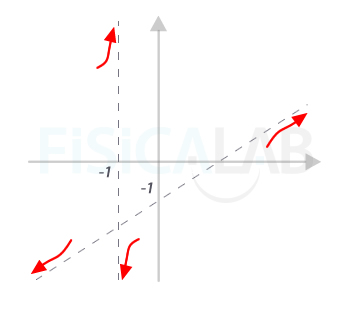
4.-

$$\boxed{f\left(x\right)=\frac{x^5+2}{3}}$$

Este caso es, en realidad, un polinomio. Observa:

$$f\left(x\right)=\frac{x^5+2}{3}=\frac{x^5}{3}+\frac{2}{3}$$

Como sabes, los polinomios no presentan asíntota de ningún tipo.

5.-

$$\boxed{f\left(x\right)=\frac{x^3}{x^2+2}}$$

Empezamos con las asíntotas verticales:

$$x^2+2=0$$

Como la ecuación anterior no tiene solución en los reales, no hay asíntotas verticales. Tampoco asíntotas horizontales:

$$\begin{gathered} \underset{x\to \infty }{\lim }\frac{x^3}{x^2+2}=\infty \\ \underset{x\to -\infty }{\lim }\frac{x^3}{x^2+2}=-\infty \end{gathered}$$

Pero sí asíntotas oblicuas:

$$\left.\begin{array}{cccc}\text{Grado}& \left(x^3\right)& =& 3\\ \text{Grado}& \left(x^2+2\right)& =& 2\end{array}\right\}\Rightarrow 3-2=1\Rightarrow \text{Asíntota Oblicua}$$

$$\frac{x^3}{x^2+2}=x+\frac{-2x}{x^2+2}$$

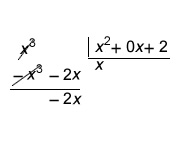
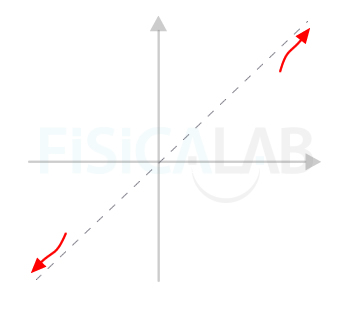
Por tanto, la ecuación de la asíntota es y=x. Para saber si la función se aproxima por encima o por debajo a la gráfica podemos dar un valor alto a la función de la ecuación y a la propia función y ver cual es superior, o bien determinar el valor de -2x/(x²+2) para valores altos de x. Así, para valores altos de x, -2x/(x²+2) resta a la asíntota, por tanto la curva quedará por debajo. Para valores muy negativos, suma, con lo que la curva quedará por encima de la asíntota. Con todos estos datos ya estamos en disposición de realizar el esbozo: