Asíntotas a partir de gráficas de funciones
Enunciado
A partir de las siguientes gráficas de funciones, determina la ecuación de las asíntas de cada una de ellas:
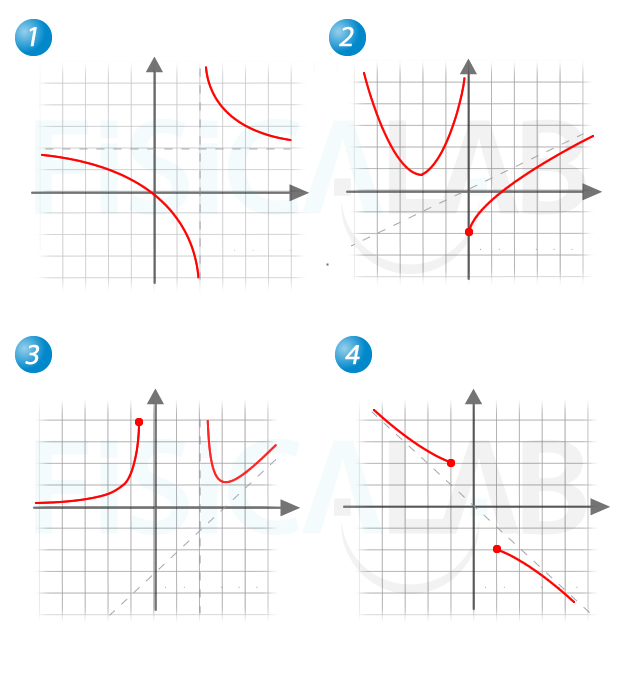
Nota: Considera que cada cuadro de las cuadrículas tiene una longitud de una unidad en horizontal y una unidad en vertical.
Solución
Consideraciones previas
Recuerda que las asíntotas verticales tienen por ecuacion x=k, las horizontales y=k y las oblicuas y=k·x+b. Se trata, simplemente, de identificar las asíntotas en las gráficas y buscar su ecuación asociada.
Resolución
1.-
La primera función presenta 2 asíntotas, una horizontal y otra vertical. Sus ecuaciones se obtienen de manera inmediata, viendo el punto de corte con el eje y y x respectivamente.
Asíntota hozirontal: y=2
Asíntota vertical: x=2
2.-
En este caso comenzamos por la asíntota oblicua, que es la más evidente. Sabemos que la ecuación explícita de una recta viene dada en la forma y=k·x+b. Observando la gráfica podemos identificar 2 puntos cualesquiera, por ejemplo:
Con lo que la ecuación de la asíntota oblicua nos queda y=x/2. Por otro lado, observando la gráfica se puede plantear la cuestión de si x=0 es una asíntota. Si no lo fuese, la rama se prolongaría a la derecha del eje y, pero entonces no habría una rama por encima y una rama por debajo de la asíntota oblícua, y eso no sería una función (recuerda que a cada valor de x le puede corresponder un único valor de y como máximo). Por tanto, x=0 es una asíntota vertical. En definitiva:
Asíntota oblicua: y=x/2
Asíntota vertical: x=0
3.-
Las asíntotas horizontal y vertical son inmediatas, para el cálculo de la oblicua nos queda:
Con lo que nos queda:
Asíntota hozirontal: y=0
Asíntota vertical: x=2
Asíntota oblicua: y=x-3
4.-
Existe una sola asíntota oblicua que calculamos como hasta ahora:
Con lo que queda:
Asíntota oblicua: y=-x
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
