Calcular punto a partir de condiciones de recta tangente a función

Consideraciones previas

Tal como hemos estudiado, la ecuación de la recta tangente a una función en un punto (a, f(a)) viene dada por la expresión:

$$y-f\left(a\right)=f\text{'}\left(a\right)·\left(x-a\right)$$

Por tanto, la pendiente de la recta tangente es justamente el valor de la derivada en x=a, es decir, f'(a). En algunos apartados, conocido el valor de f'(a), se trata de despejar a.

Por otro lado, recuerda que dos rectas son paralelas cuando tienen la misma pendiente, y que ésta puede ser calculada según el ángulo α que forma la recta con el eje de abscisas según:

$$m=\tan \left(\alpha \right)$$

Puedes determinar la ecuación de la recta que pasa por dos puntos cualesquiera P₁(x₁, y₂), P₂(x₂, y₂) a partir de la expresión:

$$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$$

Resolución

1.

$$\boxed{f\left(x\right)=\frac{1}{2x}}$$

Nos dicen que f'(a)=-1/8, es decir:

$$f\text{'}\left(x\right)=\frac{-1}{2x^2}\Rightarrow f\text{'}\left(a\right)=-1/8\Rightarrow \frac{-1}{2a^2}=\frac{-1}{8}\Rightarrow a=\pm 2$$

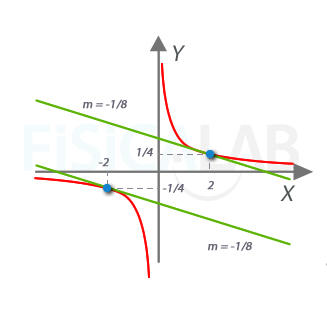
Dos rectas tangentes paralelas

En este caso existen dos puntos en los que la recta tangente a la función tiene pendiente m=-1/8: Son (-2,f(-2))=(-2,-1/4) y (2,f(2))=(2,1/4).

Si adicionalmente se nos pidiera determinar las ecuaciones de las rectas tangentes, simplemente aplicaríamos la expresión de la misma, qudando: y+1/4=(-1/8)·(x+2) para a=-2 y y-1/4=(-1/8)·(x-2) para a=2.

2.

$$\boxed{f\left(x\right)=3x^2+3x-2}$$

La bisectriz del primer cuadrante es la recta que divide el primer cuadrante del plano x-y en dos partes iguales. Por ello tiene por ecuación y=x. Como puedes ver, el factor que acompaña a la x, su pendiente, es 1. Así pues, f'(a)=1 y hay que determinar a:

$$f\left(x\right)=3x^2+3x-2\Rightarrow f\text{'}\left(a\right)=1\Rightarrow 6a+3=1\Rightarrow a=-\frac{1}{3}$$

Calculando $f\left(-1/3\right)=3{\left(-1/3\right)}^2+3\left(-1/3\right)-2=\frac{-8}{3}$, no queda que el punto considerado es (-1/3,f(-1/3))=(-1/3,-8/3).

3.

$$\boxed{f\left(x\right)=3x^2+3x-2}$$

Observa que la curva es la misma que en el apartado anterior. La particularidad de este caso es que cambia la recta. Nos la dan en la forma general Ax+By+C=0, y cuando despejamos la y nos queda:

$$3x-3y+2=0\Rightarrow 3y=3x+2\Rightarrow y=\frac{3}{3}x+\frac{2}{3}\Rightarrow y=x+\frac{2}{3}$$

La recta tiene la misma pendiente que la bisectriz del primer cuadrante (1), es decir, son paralelas, y por tanto el punto buscado es el mismo que en el apartado anterior (-1/3,f(-1/3))=(-1/3,-8/3).

4.

$$\boxed{f\left(x\right)=3x^2+3x-2}$$

De nuevo la misma función, pero esta vez nos dan el ángulo que forma la recta con el eje x. A partir de la tangente, podemos calcular el valor de la pendiente y despejar:

$$m=\tan \left(130\right)=-1.91\Rightarrow f\text{'}\left(a\right)=-1.91\Rightarrow 6a+3\Rightarrow a=-0.81$$

El punto buscado sería (-0,81, f(-0,81)), es decir (-0,81, -2.46)

5.

$$\boxed{f\left(x\right)=\frac{2}{x^2}+\frac{x}{2}}$$

Cuando una recta es horizontal, su pendiente es 0. Por tanto tenemos que derivar la función e igualarla a 0 para obtener la abscisa del punto buscado:

$$f\left(x\right)=\frac{2}{x^2}+\frac{x}{2}\Rightarrow f\text{'}\left(x\right)=\frac{-4}{x^3}+\frac{1}{2}\Rightarrow f\text{'}\left(a\right)=0\Rightarrow \frac{-4}{a^3}+\frac{1}{2}=0\Rightarrow a=2$$

Teniendo en cuenta que f(2)=3/2, el punto buscado es (2,3/2). Como veremos más adelante, los máximos y mínimos de una función cumplen precisamente que f'(a)=0, con lo que el punto (2, 3/2) podría ser un máximo o un mínimo de la función.

6.

$$\boxed{f\left(x\right)=\ln \left(x\right)}$$

En primer lugar, debemos determinar la expresión de la recta que pasa por los puntos señalados, para saber su pendiente. Para determinar la ecuación de la recta que pasa por los puntos señalados utilizaremos la expresión ya recogida en las consideraciones previas $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$&nsbp;. Siendo los puntos (1,1) y (e,2), podemos identificar x₁=1, x₂=e, y₁=1 y y₂=2. La expresión de la recta secante a ambos puntos queda, por tanto:

$$\frac{x-1}{e-1}=\frac{y-2}{2-1}\Rightarrow y=\frac{x}{e-1}-\frac{1}{e-1}+2$$

La pendiente es el cociente 1/(e-1). Busquemos ahora f'(a) para obtener el punto buscado:

$$f\text{'}\left(x\right)=\frac{1}{x}\Rightarrow f\text{'}\left(a\right)=\frac{1}{a}\Rightarrow \frac{1}{e-1}=\frac{1}{a}\Rightarrow a=e-1$$

El punto considerado, es por tanto $f\left(e-1\right)=\ln \left(e-1\right)\Rightarrow \left(e-1, \ln \left(e-1\right)\right)$

7.

$$\boxed{f\left(x\right)=2\sin \left(x^2\right)}$$

Comenzamos calculando f'(a):

$$f\left(x\right)=2\sin \left(x^2\right)\Rightarrow f\text{'}\left(x\right)=4x\cos \left(x^2\right)\Rightarrow f\text{'}\left(a\right)=4a\cos \left(a^2\right)$$

Igualamos al valor de pendiente considerado:

$$4a\cos \left(a^2\right)=-4\sqrt{\mathrm{\pi }}$$

Sabemos que el coseno oscila entre -1 y 1, con lo que debemos prestar atención al factor 4a. Observa:

$$a=\sqrt{\mathrm{\pi }}\Rightarrow \cos \left(a^2\right)=-1\Rightarrow f\text{'}\left(\sqrt{\mathrm{\pi }}\right)=-4\sqrt{\mathrm{\pi }}$$

Con lo que el punto considerado es:

$$f\left(\sqrt{\mathrm{\pi }}\right)=2\sin \left({\left(\sqrt{\mathrm{\pi }}\right)}^2\right)=0\Rightarrow \left(\sqrt{\mathrm{\pi }},0\right)$$