Dominio de funciones irracionales

Consideraciones previas

Las raices de índice par no pueden ser negativas, por lo que restringiremos el dominio a aquellos valores de x que cumplan esta condición. En el caso de que el radicando ("lo que hay dentro de la raíz") sea un polinomio de primer grado, la resolución de la inecuación es inmediata, como veremos. Para el caso de polinomios de mayor grado, recurriremos a un cuadro de signos. Estos son muy útiles siempre que la función pueda descomponerse en productos o cocientes de productos y nos indican el signo de la función en distintos intervalos de x.

Para descomponer en productos o cocientes de productos los polinomios de grado mayor de dos utilizamos Ruffini o, en el caso concreto de un polinomio de segundo grado, la resolución de una ecuación de segundo grado.

Puedes estudiar las funciones irracionales en profundidad en el apartado enlazado.

Solución

$$\boxed{f\left(x\right)=\sqrt{x+1}}$$

$$x+1⩾0\Rightarrow x⩾-1\Rightarrow Do{m}_f=[-1,\infty )$$

$$\boxed{f\left(x\right)=\sqrt{1-x}}$$

$$1-x⩾0\Rightarrow -x⩾-1\Rightarrow x⩽1\Rightarrow Do{m}_f=(-\infty ,1]$$

$$\boxed{f\left(x\right)=\sqrt{3x-2}}$$

$$3x-2⩾0\Rightarrow 3x⩾2\Rightarrow x⩾\frac{2}{3}\Rightarrow Do{m}_f=[2/3,\infty )$$

$$\boxed{f\left(x\right)=\sqrt{-3x^2+5x-2}}$$

Tenemos que resolver la inecuación -3x²+5x-2⩾0. Lo haremos mediante la tabla o cuadro de signos. Para comenzar factorizamos el radicando:

$$\begin{gathered} -3x^2+5x-2=0\Rightarrow x=\frac{-5\pm \sqrt{5^2-4\left(-3\right)\left(-2\right)}}{2·\left(-3\right)}=\left\{\begin{array}{l}{x}_1=1\\ x_2=2/3\end{array}\right.\Rightarrow \\ \Rightarrow -3x^2+5x-2=-3\left(x-1\right)·\left(x-\frac{2}{3}\right) \end{gathered}$$

A partir de las dos raíces del polinomio (los valores de x que lo hacen 0) podemos distinguir 3 intervalos. En cada intervalo el polinomio tiene un signo. Mediante la tabla estudiamos el signo de cada factor (primera columna), en cada uno de los intervalos (primera fila), para así averiguar el signo del polinomio total en tales intervalos (última fila). Veamos:

Observa que para averiguar el signo de cada factor con forma (x-a), en las dos primeras filas, hemos tomado un valor al azar en ese intervalo y hemos obtenido el signo del factor. Para el signo del producto, en la tercera fila, multiplicamos los signos de las celdas de la misma columna de las filas anteriores, es decir, multiplicamos el signo de los factores (x-2/3)·(x-1). Finalmente, como hay un factor -3, en la última fila cambiamos los signos.

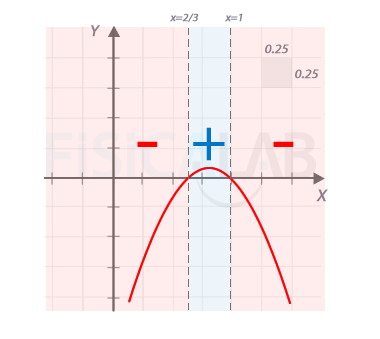
Signo de la parábola

Puedes visualizar el signo de la parábola en cada intervalo representando en una gráfica el polinomio del radicando, . Para ello observa si la parábola está por encima (signo positivo) o por debajo del eje x (signo negativo). Los puntos de corte con el eje x son precisamente los puntos en los que la parábola cambia de signo.

En definitiva:

$$Do{m}_f=[2/3,1]$$

Donde hemos incluido en el dominio las propias raíces del polinomio (extremos cerrados en 2/3 y en 1), porque en ellas el polinomio se anula, y la raíz cuadrada de cero no es un valor a restringir en el dominio.

$$\boxed{f\left(x\right)=\sqrt{3x^2-5x+2}}$$

En este caso tenemos una parábola como polinomio del radicando que es similar a la anterior, pero con las ramas hacia arriba. Es decir, $3x^2-5x+2=-\left(-3x^2+5x-2\right)$

El proceso de factorización:

$$\begin{gathered} 3x^2-5x+2=0\Rightarrow x=\frac{5\pm \sqrt{{\left(-5\right)}^2-4\left(3\right)\left(2\right)}}{2·3}=\left\{\begin{array}{l}{x}_1=1\\ x_2=2/3\end{array}\right.\Rightarrow \\ \Rightarrow 3x^2-5x+2=3\left(x-1\right)·\left(x-\frac{2}{3}\right) \end{gathered}$$

Ahora usamos la tabla de signos para resolver la inecuación $3x^2-5x+2\ge 0$, que es, en definitiva, la que nos permite obtener los valores incluidos en el dominio:

En este caso no es necesaria una última fila para multiplicar el factor 3, ya que este no cambia el signo. Por tanto:

$$Do{m}_f=(-\infty ,2/3]\cup [1,\infty )$$

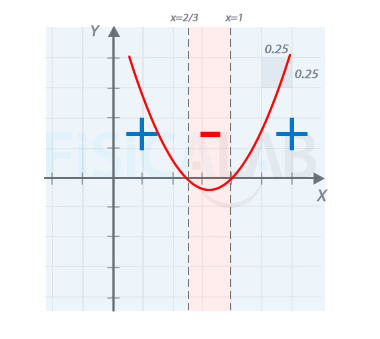
Signo de la parábola

Puedes visualizar el signo de la parábola en cada intervalo representando en una gráfica el polinomio del radicando. En este caso, las raíces son las mismas (puntos en los que se anula la parábola) que en el caso anterior, pero la parábola tiene las ramas hacia arriba con lo que los signos son los complementarios en cada intervalo.

$$\boxed{f\left(x\right)=\sqrt{x^2-9}}$$

En este caso, la factorización podríamos hacerla de nuevo resolviendo una ecuación de segundo grado, pero también recordando las identidades notables:

$$x^2-9=x^2-3^2\underset{a^2-b^2=\left(a+b\right)\left(a-b\right)}{=}(x+3)\left(x-3\right)$$

Es decir, las raíces del polinomio son -3 y 3. Aplicando el cuadro de signos para resolver la inecuación $x^2-9\ge 0$:

Tomando los valores positivos de la última fila obtenemos el dominio:

$$Do{m}_f=(-\infty ,-3]\cup [3,\infty )$$

$$\boxed{f\left(x\right)=\sqrt{x^2+3x}}$$

De nuevo, un polinomio de segundo grado como radicando, que en esta ocasión factorizaremos sacando factor común la x.

$$x^2+3x=x\left(x+3\right)$$

Las raíces, por tanto son -3 y 0. Aplicando la tabla de signos:

Para el dominio nos quedamos con la parte positiva:

$$Do{m}_f=(-\infty ,-3]\cup [0,\infty )$$

$$\boxed{f\left(x\right)=\sqrt[128]{2x^3+14x^2+8x-24}}$$

En este caso nos puede llamar la atención el índice de la raíz. Al ser de índice par, la restricción es la misma que para las raíces cuadradas, es decir, el radicando debe ser mayor o igual que cero. En este caso el radicando es un polinomio de grado 3. Lo factorizaremos por Ruffini:

$$\begin{gathered} 2x^3+14x^2+8x-24=0\Rightarrow \begin{array}{ccccc}& 2& 14& 8& -24\\ 1& & 2& 16& 24\\ & 2& 16& 24& 0\\ -2& & -4& -24& \\ & 2& 12& 0& \end{array}\Rightarrow \\ \Rightarrow 2x^3+14x^2+8x-24=\left(x-1\right)\left(x+2\right)\left(2x+12\right)=2\left(x-1\right)\left(x+2\right)\left(x+6\right) \end{gathered}$$

Podemos aplicar de nuevo la tabla de signos para resolver $2x^3+14x^2+8x-24\ge 0$, sabiendo que las raíces son -6, -2 y 1:

Quedando el dominio:

$$Do{m}_f=[-6,-2]\cup [1,\infty )$$

$$\boxed{f\left(x\right)=\sqrt[3]{-3x^2+5x-2}}$$

Es una raíz cúbica en cuyo radicando hay un polinomio. Las raíces de índice impar no imponen ninguna restricción al dominio, el polinomio tampoco, con lo que:

$$Do{m}_f=\mathrm{ℝ}$$