Representación gráfica mediante transformación de funciones elementales

Resolución

$$\boxed{f\left(x\right)=\sqrt{1-x}}$$

Partimos de la función de tipo raíz cuadrada $g\left(x\right)=\sqrt{x}$, cuya gráfica debemos conocer, y aplicamos:

$$g\left(x\right)=\sqrt{x}\Rightarrow g\left(1-x\right)=\sqrt{1-x}=f\left(x\right)$$

Esto significa un desplazamiento horizontal a la izquierda de 1 unidad y posteriormente una inversión horizontal. Recuerda seguir el orden propuesto en teoría, para que no haya errores.

$$\boxed{f\left(x\right)={\left(2x-3\right)}^2+1}$$

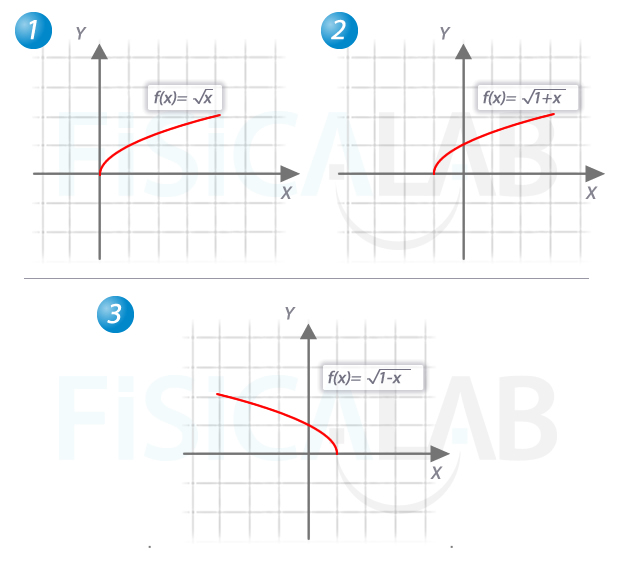
Esta vez partimos de la función $g\left(x\right)=x^2$, cuya gráfica también debemos conocer, y aplicamos:

$$g\left(x\right)=x^2\Rightarrow g\left(2x-3\right)+1={\left(2x-3\right)}^2+1=f\left(x\right)$$

Esto implica un desplazamiento horizontal a la derecha de 3 unidades, una contracción horizontal de magnitud 2 y un desplazamiento vertical de 1 unidad hacia arriba (en el orden propuesto todo ello).

$$\boxed{f\left(x\right)=3·e^{-\frac{x}{2}}}$$

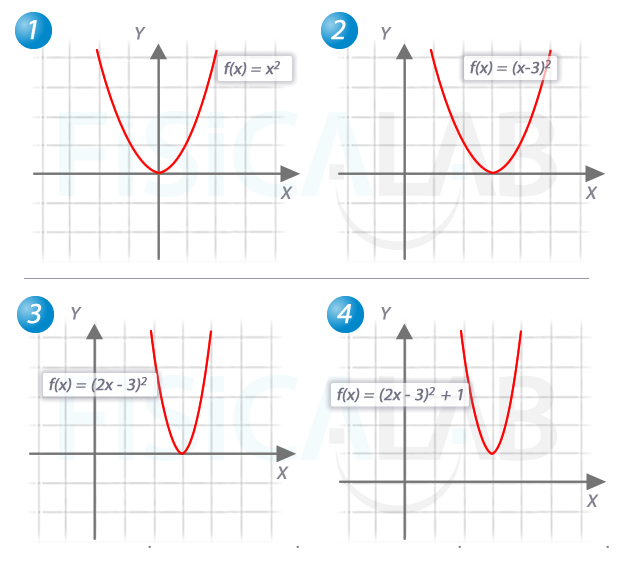
La función exponencial $g\left(x\right)=e^x$ es la que nos sirve esta vez de punto de partida:

$$g\left(x\right)=e^x\Rightarrow 3·g\left(-x/2\right)=3·e^{-\frac{x}{2}}=f\left(x\right)$$

La cadena de transformaciones propuesta es: expansión horizontal de magnitud 1/2, reflexión horizontal y expansión vertical de magnitud 3.

$$\boxed{f\left(x\right)=-\ln \left(\frac{x}{3}+1\right)+2}$$

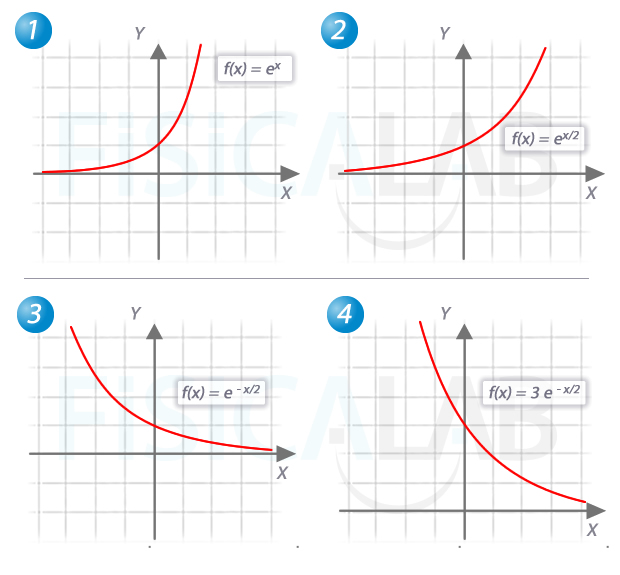
En este caso la función de partida es de tipo logaritmo neperiano, $g\left(x\right)=\ln \left(x\right)$, que debe ser transformada según:

$$g\left(x\right)=\ln \left(x\right)\Rightarrow -g\left(\frac{x}{3}+1\right)+2=-\ln \left(\frac{x}{3}+1\right)+2=f\left(x\right)$$

Esto implica comenzar desplazando horizontalmente 1 unidad hacia la izquierda la función g(x), realizar una expansión horizontal de magnitud 1/3, posteriormente invertir verticalmente la función y, finalmente, desplazarla dos unidades hacia arriba.

$$f\left(x\right)=\cos \left(\frac{x+2}{2}\right)$$

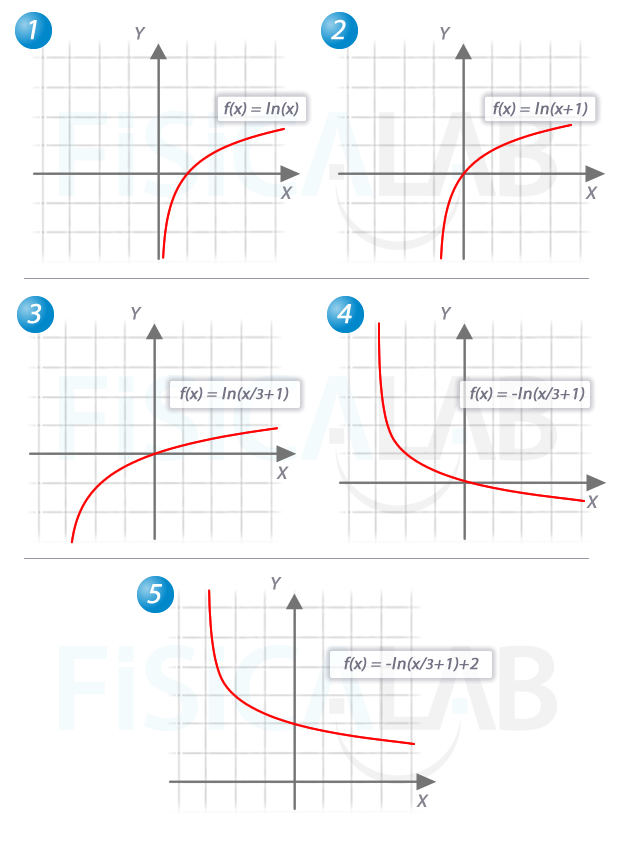
En primer lugar, debemos hacer alguna transformación previa para dejarla en la forma que hemos visto en teoría que nos va a permitir seguir el orden de transformaciones propuesto:

$$f\left(x\right)=\cos \left(\frac{x+2}{2}\right)=\cos \left(\frac{x}{2}+1\right)$$

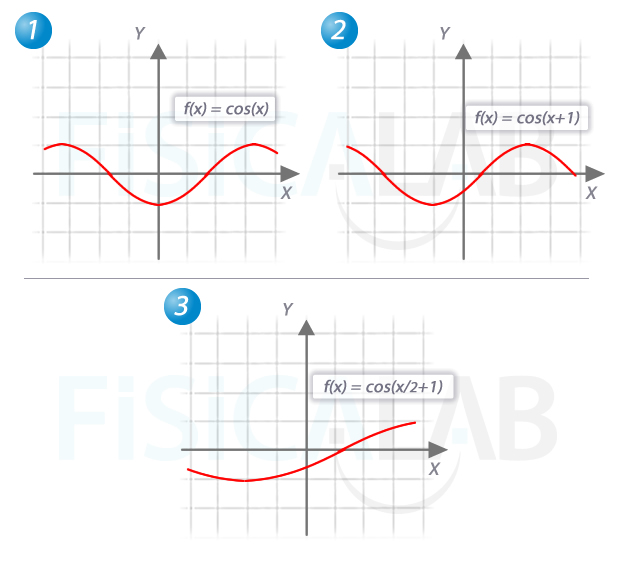
Utilizando como referencia la función $g\left(x\right)=\cos \left(x\right)$, podemos escribir:

$$g\left(x\right)=\cos \left(x\right)\Rightarrow g\left(\frac{x}{2}+1\right)=\cos \left(\frac{x}{2}+1\right)=f\left(x\right)$$

Esto implica comenzar con un desplazamiento horizontal de 1 unidad hacia la izquierda, y una expansión de magnitud 1/2.