Determina la inversa gráficamente
Enunciado
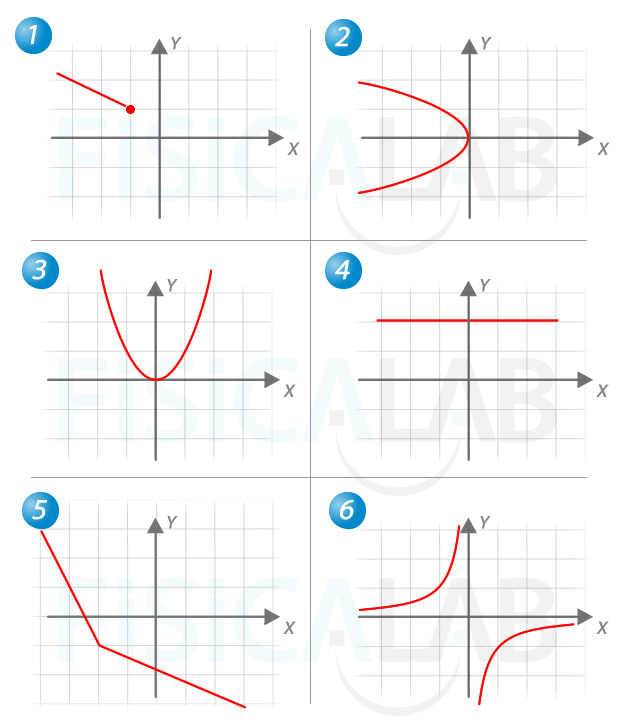
Determina la gráfica de la función inversa en los siguientes casos:
Solución
Consideraciones previas
En primer lugar, sabemos una función tiene inversa si es inyectiva, esto es, ninguna recta horizontal puede atravesarla en más de 1 punto. De esta manera podemos descartar las funciones 3 y 4, como veremos posteriormente.
Por otro lado, para representar las inversas de las funciones dadas debemos recordar que estas son simétricas respecto a la recta y=x. Es importante recordar que un punto arbitrario (a,b) de la función original se convertirá en un punto (b,a) en su inversa.
Resolución
1.-
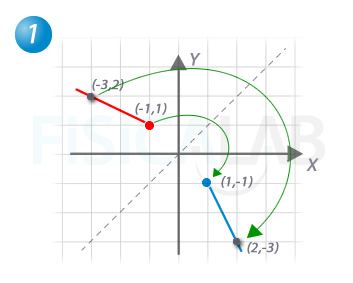
Resolución del primer apartado
La función original, en rojo, tiene como inversa la función en azul. Para encontrarla, dado que es una recta, trasladamos dos puntos arbitrarios -el (-1,1) y el (-3,2) -a sus simétricos respecto a la recta y=x representada en modo discontínuo.
2.-
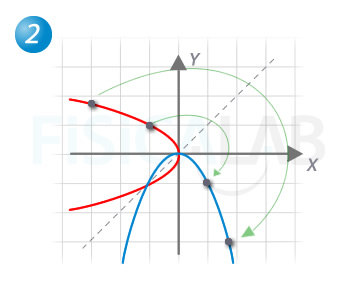
Resolución de la segunda función
La función original, en rojo, tiene como inversa la función en azul. Para encontrarla, trasladamos dos o más puntos arbitrarios y rehacemos la gráfica en la nueva posición. ¿Sabrías decir que a qué expresión analítica corresponde cada función?
3.-
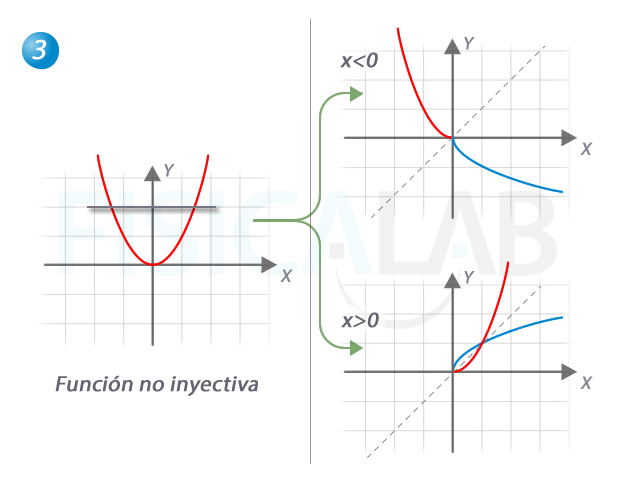
Resolución de la tercera función
En esa ocasión la función original no tiene inversa, pues no es inyectiva. Sin embargo, podemos descomponerla en dos ramas que sí son invectivas. Una para los x<0 y otra para los x>0.
4.-
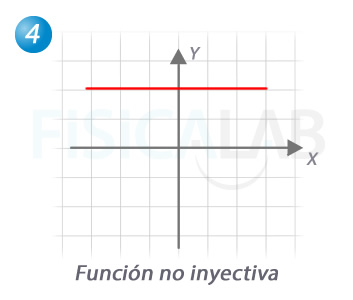
Resolución de la cuarta función
En este caso, estamos ante una recta horizontal. No es inyectiva y no tiene sentido que hablemos de función inversa. De hecho, si trasladásemos varios puntos arbitrarios, como hemos hecho hasta ahora, obtendríamos una recta x=2, que no es una función (a un valor de x corresponden infinitos valores de y).
5.-
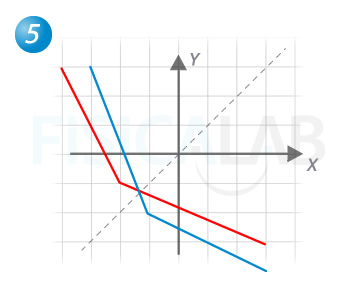
Resolución de la quinta función
En este caso, siguiendo un proceso similar, obtenemos la función en azul.
6.-
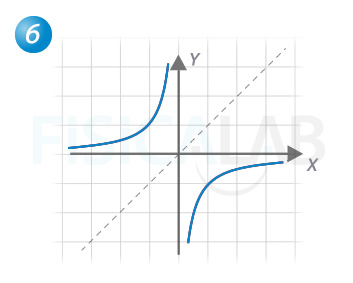
Resolución de la sexta función
Como puedes comprobar, si buscamos la función simétrica de la primera función respecto a la recta y=x llegamos a una gráfica igual a la original. Efectivamente, la funcion f(x)=1/x correspondiente a la función original, en rojo, tiene por simétrica la propia función 1/x ya que
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
