Interpretación gráfica de la derivada
Enunciado
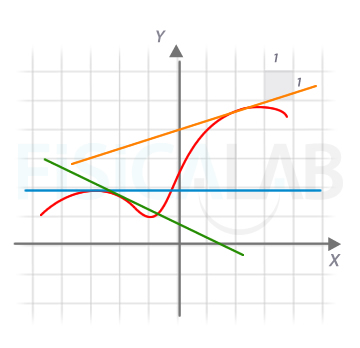
Calcula f'(-3), f'(2) y f'(-2) a partir de la información de la gráfica de f(x), en rojo, en la siguiente imagen:
Solución
Consideraciones previas
Recuerda que la derivada de una función en un punto es la pendiente de la recta tangente a la función en dicho punto
Expresamos la pendiente de una recta que pasa por dos puntos (x1, y1), (x2, y2) de la siguiente manera:
Si deseas profundizar sobre la interpretación gráfica de la derivada, una vez terminado este ejercicio, visita el siguiente.
Resolución
1. En f'(-3) la pendiente de la recta tangente, en azul, es 0, porque la recta es horizontal. Por tanto f'(-3)=0.
2. Para calcular f'(2), es decir, la pendiente de la recta tangente, en naranja en este caso, que pasa por el punto con abscisa x=2 de la función f(x), cogemos dos puntos cualesquiera de la recta en el punto y los usamos en la formula
3. Calculamos ahora f'(-2). Para la recta tangente, en verde, resulta más complicado encontrar puntos discretos (valores enteros) para el cálculo de su pendiente. Podemos usar los siguientes, (-0.5, 1) y (1.5, 0), quedando:
Observa que, en este último caso podríamos haber llegado a la misma conclusión teniendo presente que la recta tangente decrece una unidad vertical por cada dos horizontales, con lo que m=-1/2.
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
