Relacionar cada gráfica con su derivada
Enunciado
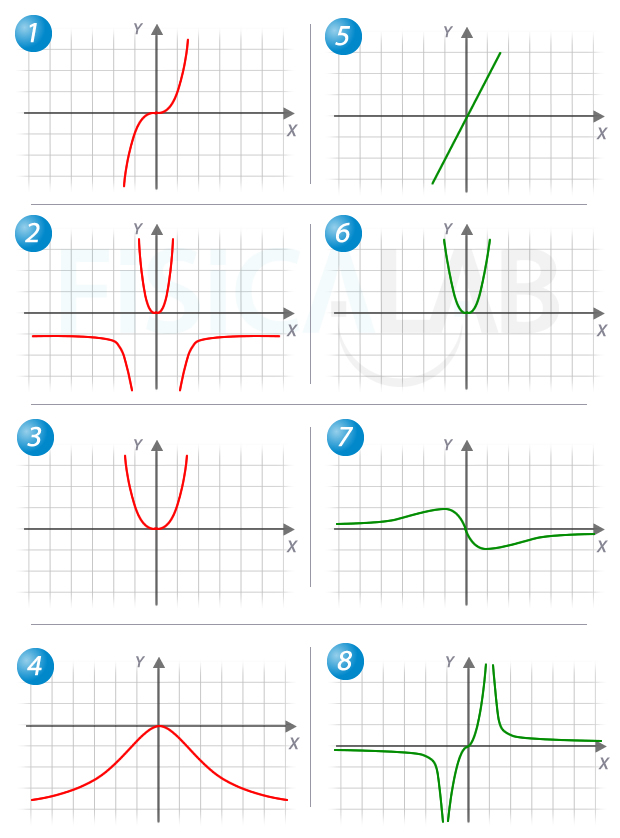
Relaciona cada gráfica de la columna izquierda, con su derivada en la columna derecha.
Solución
Consideraciones previas
Recuerda que la función derivada de otra dada asocia a cada punto de la misma el valor de la pendiente de su recta tangente.
Te recomendamos que imagines la recta tangente en cada punto de las gráficas izquierdas, y pienses en su pendiente, es decir, su inclinación. Recuerda que si la tangente crece, la derivada debe ser positiva, y si decrece la derivada debe decrecer. En los puntos en los que no esté definida la función, tampoco lo estará la derivada.
Resolución
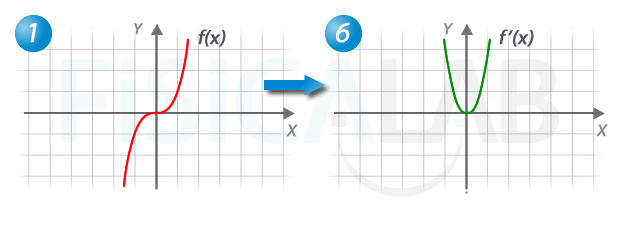
Efectivamente, la gráfica original corresponde a un polinomio de grado 3, cuya derivada es una parábola. Si lo observas, la pendiente de la recta tangente en puntos "a la izquierda" de la gráfica original es muy positiva, después va poniéndose horizontal, y luego iría haciéndose de nuevo positiva. Si tomásemos los valores de las pendientes de dichas rectas tangentes obtendríamos una parábola, que es la gráfica asociada a la derecha.
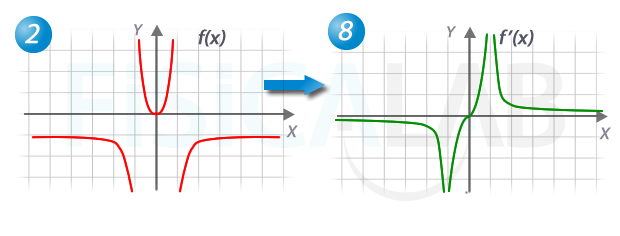
Este caso es inmediato, pues la gráfica en 8 es la única que no está definida en los puntos en los que tampoco lo está la función 2, por ser asíntotas verticales.
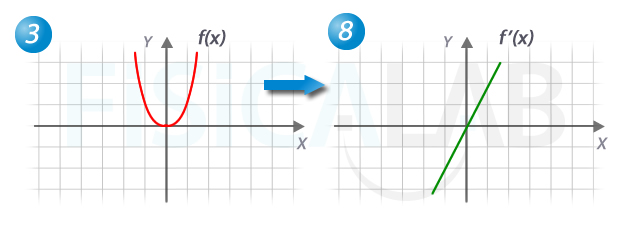
En el caso de la función 3, parece ser una parábola, es decir, un polinomio de grado 2, con lo que su derivada será una recta, es decir, un polinomio de grado 1. También puedes observar que la pendiente de la recta tangente siempre es creciente, y negativa en el caso de que x<0.
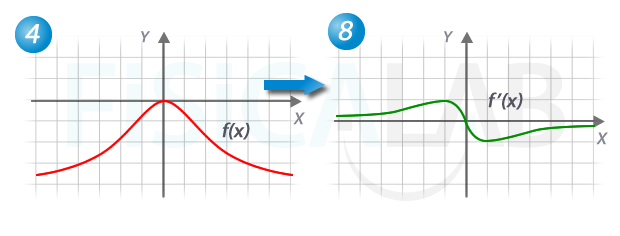
En el último caso observa (imaginariamente) el comportamiento de la pendiente de recta tangente, y comprobarás que, efectivamente, corresponde a la función en 8. La pendiente tiene pendiente 0 en x=0, a la izquierda es negativa y a la derecha positiva, pero con distintos valores según el x considerado.
Nota: Después de haber realizado este ejercicio es bueno que te des cuenta de que si cualquiera de las funciones de la columna izquierda estuvieran situadas varias unidades por encima o varias unidades por debajo, su función derivada no variaría, ya que esta solo tiene en cuenta el comportamiento de la recta tangente, que no variaría. Es por ello que D(f(x)) = D(f(x)+k) siendo k una constante cualquiera.
No hemos encontrado ninguna fórmula destacable en este ejercicio.
