Interpretación gráfica avanzada de la derivada
Enunciado
Sabiendo que la siguiente gráfica corresponde a la derivada de f(x), f'(x), ¿cuánto vale la pendiente de la recta tangente a f(x) en x=0?
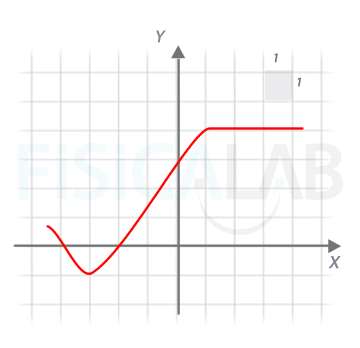
Y si la gráfica correspondiese directamente a f(x), ¿cuál será el valor de f'(3)?
¿Cuáles serán los puntos de derivada nula?
¿Cuál es el valor de x si f(x)=-1
Solución
Consideraciones previas
La base para la interpretación de la gráfica en este ejercicio, es recordar que la derivada f'(x) de una función f(x) en un punto, es la pendiente de la recta tangente a la función en dicho punto.
Si la resolución de este ejercicio te resulta complicada, visita este ejercicio básico sobre el tema.
Resolución
Sabiendo que la siguiente gráfica corresponde a la derivada de f(x), f'(x), entonces,¿cuánto vale la pendiente de la recta tangente a f(x) en x=0?
Para calcular el valor de la pendiente de la recta tangente a f(x) en x=0 miramos la gráfica y nos damos cuenta que para x=0, y=3, por lo tanto el valor de la pendiente de la recta tangente será 3.
Y si la gráfica correspondiese directamente a f(x), ¿cuál será el valor de f'(3)?
Siendo la gráfica dada f(x),calculamos el valor de f'(3). Para ello hay que fijarse en el punto de la gráfica en x=3. Lo situamos y nos damos cuenta que por la gráfica en ese punto la línea tangente es horizontal(es decir de pendiente 0). Por tanto f'(3)=0.
¿Cuáles serán los puntos de derivada nula?
Para identificar los puntos de derivada nula (puntos donde la derivada vale 0) tenemos que buscar aquellos puntos en los que la recta tangente a la función sea horizontal (pendiente 0). Esto se cumple en el punto f(-3), pero también en aquellos valores de x mayores que 1, por tanto:
¿Cuál es el valor de x si f(x)=-1?
Esta cuestión no tiene relación con la derivada. Buscamos el valor para el que f(x) vale -1. Este punto corresponde a x=-3.
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
