Statement
A broken faucet lets out water drops every 1/4 of a second. If the faucet is just 3 meters above the ground, and if one drop falls in this very instant, determine what is the position of the drops still in the air at this moment.
Solution
Data
H = 3 m
g = 9.8 m/s2
Time that each drop has been in the air
t0=0 s, t1=0.25 s, t2=0.5 s, t3=0.75 s, t4=1 sg, etc...
y0, y1, y2, y3, ... ?
Resolution
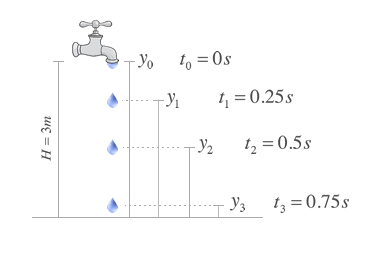
Let us call y0, y1, y2... the positions of each drop in the air, starting with the one still exiting the faucet as it is shown in the figure. In the same way, let us call t0, t1, t2, etc... the time each of these drops has been in the air.
Applying the formula of the position in fall free motion, for each drop, we get that:
As you can see, the position of drop y4 is a negative number, so, if the ground is y=0, then the drop reached the ground at some prior time and therefore, it is not in the air at this moment. From that we reason that there are only 4 drops still falling.

