The uniformly accelerated rectilinear motion (u.a.r.m.), also known as constant acceleration motion, is a rectilinear motion that has a constant acceleration, which is different from zero. In this section we are going to study:
- The concept and properties of the constant acceleration motion
- The equations of constant acceleration motion
- How to derive the equations
- Merton’s Theorem
Concept of constant acceleration motion
The constant acceleration motion is quite common in your daily life. An object that is allowed to fall and that does not find any obstacle in its way (free fall), or a skier that descends an incline, just before arriving to the jump area, are good examples of this. The constant acceleration motion or uniformly accelerated rectilinear motion (u.a.r.m) has the following properties:
- The trajectory is a straight line and therefore the normal or centripetal acceleration is zero
- The instantaneous velocity changes its magnitude (speed) uniformly: it increases or decreases by the same amount in each unit of time. This implies the following point
- The tangential acceleration is constant. Therefore average acceleration is the same as instantaneous acceleration for any period studied (
A body moves with constant acceleration motion or uniformly accelerated rectilinear motion (u.a.r.m) when its trajectory is a straight line and its acceleration is constant and different from 0. This implies that the velocity increases or decreases its magnitude uniformly.
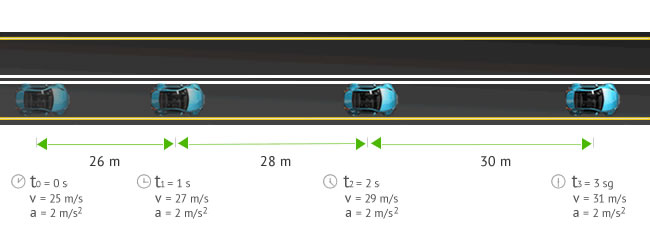
Uniformly Accelerated Rectilinear Motion
In our example the car describes a u.a.r.m since it moves in a straight line with a constant acceleration equivalent to 2 m/s2. [Notice that, in each second, the velocity and the distance traveled by the body increase based on the value of the acceleration in the previous second.]
Notice that although colloquially, we make distinction between an accelerating and a braking body, from the point of view of physics, both are uniformly accelerated rectilinear motions. The difference is that while one has positive acceleration, the other one has negative acceleration.
Constant acceleration motion equations
The equations of the constant acceleration motion or uniformly accelerated rectilinear motion (u.a.r.m.) are:
Where:
- x, x0: Position of the body at a given time (x) and at the initial time (x0). Its unit in the International System (SI) is the meter (m)
- v,v0: Velocity of the body at a given time (v) and at the initial time (v0). Its unit in the International System is meter per second (m/s)
- a: Acceleration of the body. Remains constant with a value different from 0. Its unit in the International System is meter per second (m/s2)
- t: Time being studied. Its unit in the International System is the second (s)
Although the former are the main equations of the u.a.r.m. and the only ones necessary to solve the exercises, it is sometimes useful know the following expression:
The above formula allows you to relate velocity and distance traveled if the acceleration is known, and can be deduced from the previous ones, as you can see below.
Deduction of the constant acceleration motion equations
To deduce the equations of constant acceleration motion or uniformly accelerated rectilinear movement (u.a.r.m), it must be taken into consideration that:
- The normal or centripetal acceleration value is zero:
- The average acceleration, instant acceleration and tangential acceleration have the same value:
With these restrictions, we get:
This first equation relates velocity of a body with its acceleration at any given time and represents a straight line (v) whose slope is the same as the magnitude of the acceleration and its y coordinate at the origin is the initial velocity (v0). We need to get an equation that allows us to obtain the position. There are different methods to deduce it. We will use the mean speed theorem or Merton rule of uniform acceleration:
"A body with uniformly accelerated motion travels, in any given time, the same distance that would be traveled by a body moving with a constant velocity equal to the average velocity of the first body."
This means that
The value of the average velocity, when the acceleration is constant, can be clearly observed in the following figure:
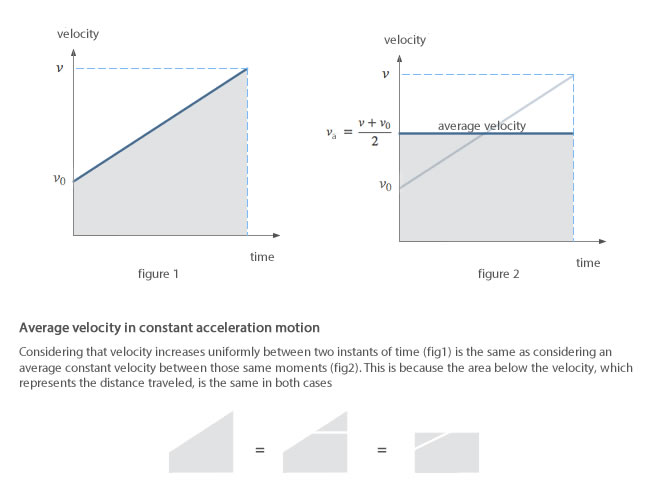
If we develop the equations we have seen so far, we obtain the equation of the position in the uniformly accelerated rectilinear motion (u.a.r.m.):
Where have we applied:
Finally, notice that in the previous equations the motion has been considered in the x-axis. If we move in the y-axis, for example in free fall or vertical launch motions, simply substitute x with y for the position, resulting in the following equation:

