Ayúdanos a mantenernos en órbita
¿Nuestros contenidos te están resultando de utilidad?
Con un pequeño gesto podremos mantenernos en órbita. Regístrate para acceder a contenidos y funcionalidad exclusiva. Además, con tu ayuda podremos continuar ofreciendo nuestros servicios de manera gratuita para miles de estudiantes en todo el mundo. Te ofrecemos:
- Un campus virtual orientado a la gamificación
- Nuevos contenidos premium
- Nuevas simulaciones
- Acceso prioritario a nuestro plantel de profesores de física y matemáticas
Among all the constant acceleration motions, or uniformly accelerated rectilinear movements (u.a.r.m.), there are two of particular interest: free fall and vertical launch. In this section, we will study vertical launch. Both are governed by the equations of the uniformly accelerated rectilinear motion (u.a.r.m.):
Vertical launch
In vertical launch, an object is launched vertically up or down from a height H without taking into consideration any kind of friction with the air or any other obstacle. It is a uniformly accelerated rectilinear motion (u.a.r.m.) in which the acceleration is gravity. On the surface of the Earth, the acceleration of gravity can be considered constant and directed downward. It is designated by the letter g, and its value is 9.8 m/s2.
To study vertical launch motion, normally, we will use a system of reference whose origin of coordinates is located at the base of the positive y-axis, as can be seen in the picture.
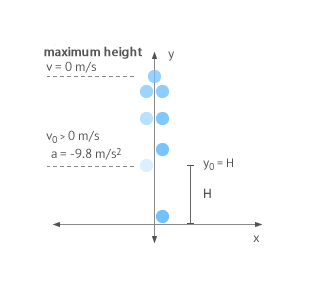
Vertical launch upward
The body is launched upward from a height H, with a velocity greater than 0. As it ascends, its speed decreases until it reaches 0 (maximum height). From that point onwards, its velocity is negative and it begins to descend.
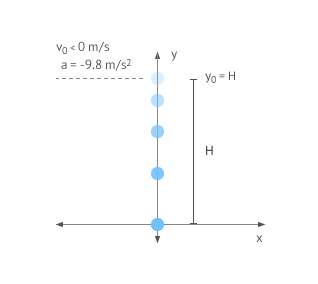
Vertical launch down
The body is launched downwards from a height H, with a speed smaller than 0 which will remain negative throughout the entire motion.
The vertical launch is a uniformly accelerated rectilinear motion (u.a.r.m.) or constant acceleration motion in which a body is launched vertically with some initial velocity from a certain height and do not find any resistance on its way. We can distinguish two cases based on the system of reference considered:
-
We launch the body upward and therefore the initial velocity is positive (v0>0). In this case the equations for the upward vertical launch are:
-
We launch the body downward and therefore the initial velocity is negative (v0<0). In this case the equations for the downward vertical launch are:
Where:
- y: Final position of the body. Its unit in the International System (SI) is the meter (m)
- v, v0: The final and initial velocity of the body respectively. Its unit in the International System (SI) is the meter per second (m/s)
- a: Acceleration of the body while in motion. Its unit in the International System (SI) is the meter per second squared (m/s2)
- t: Time spent on the motion. Its unit in the International System (SI) is the second (s)
- H: Height from which the body is launched. It is a measurement of length and therefore is unit is the meter (m)
- g: Value of the gravitational acceleration which on Earth surface can be considered equal to 9.8 m/s2