Momentum Conservation Principle

Conservation principles are the Physics´ fundamental laws and they are basic to understand many everyday phenomenom. In particular, the conservation principle of linear momentum is a consequence of the action - reaction principle or Newton´s third law.

Demostration

Think of two bodies isolated, A and B, with just one interaction between them. According to the action - reaction principle:

$${\overrightarrow{F}}_{AB}=-{\overrightarrow{F}}_{BA}$$

Knowing that $\overrightarrow{F}=\frac{∆\overrightarrow{p}}{∆t}$, then:

$$\begin{gathered} \frac{∆{\overrightarrow{p}}_A}{∆t}=\frac{-∆{\overrightarrow{p}}_B}{∆t}\Rightarrow \\ \frac{∆\left({\overrightarrow{p}}_A+{\overrightarrow{p}}_B\right)}{∆t}=0 \end{gathered}$$

This expression tells us the variation of the sum of the momentums is void, thus the total linear momentum of both bodies remains constant:

$${\overrightarrow{p}}_A+{\overrightarrow{p}}_B = \text{constant}$$

Differential notation

We have already explained in several occasions that, in mathematical language, when a magnitude remains constant in time has a derivative equal to zero in relation to that one. So, in this case we may write:

$$\boxed{\sum \overrightarrow{F}=0 \iff \frac{d\overrightarrow{p}}{dt}=0}$$

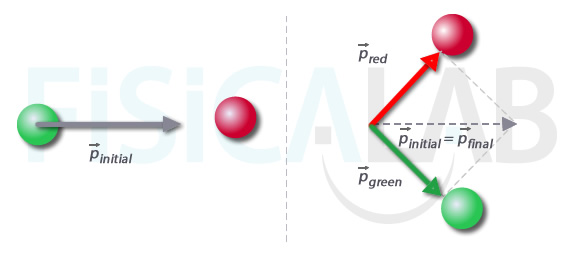
Collisions and explosions

In physics we say that an isolated system is the one with no interaction with the outside, thus it is not subdue to external forces in relation to it. Particles taking part in crashes, explosions, reaction engines, etc, can be consider isolated systems in which external forces may be disregard opposite to the intensity of the inner ones. Conservation of momentum principle has an important aplication in the study of those phenomenoms, when we don´t know the causes that originate them, since, before and after the phenomenom of linear momentum of the whole system...

$${\overrightarrow{p}}_{\mathrm{before}}={\overrightarrow{p}}_{\mathrm{after}}$$

Laws of Newton

As we saw in the previous demonstration, we can consider the conservation of momentum principle as a direct consequence of the Newton´s third law. Therefore, if we apply it on a body whose mass does not vary, it is equivalent to the Newton´s first law:

$$\sum \overrightarrow{F}=0 \iff \frac{d\overrightarrow{p}}{dt}=0\underset{\begin{array}{c}\overrightarrow{p}=m·\overrightarrow{v}\\ m=cnt\ne 0\end{array}}{\iff }m·\frac{d\overrightarrow{v}}{dt}=0\iff \overrightarrow{v}=cnt$$